Use Databin to Store Time Series
The arrival times in a PoissonProcess are independent and follow an ExponentialDistribution. You can simulate a path of a PoissonProcess by sending signals to a Databin in time intervals specified by a simulation of an exponential distribution.

SeedRandom["11"];
\[Lambda] = 0.5;
times = RandomVariate[ExponentialDistribution[\[Lambda]], 30];Create a Databin.
bin = CreateDatabin[]Use the simulated times to send 1 to the databin in time intervals.
Table[DatabinAdd[bin, <|"arrivals" -> 1|>]; Pause[t], {t, times}];The recorded signal with the time stamps.
TimeSeries[bin]Extract the TimeSeries object.
ts1 = TimeSeries[bin]["arrivals"]This time series is irregularly sampled.
RegularlySampledQ[ts1]Assume TemporalRegularity so that Accumulate does not use interpolation to resample the time series with respect to the minimum time increment.
ts2 = Accumulate[TimeSeries[ts1, TemporalRegularity -> True]]DateListStepPlot[ts2, Joined -> False, PlotTheme -> "Detailed"]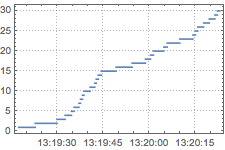
Estimate the PoissonProcess parameter from the signal and compare to the parameter of the ExponentialDistribution used to simulate time stamps.
{FindProcessParameters[ts2, PoissonProcess[\[Mu]]], \[Lambda]}