Analyze Kirkwood Gaps in the Asteroid Belt
Asteroids are a major subset of the minor planets found throughout the solar system. A majority of them are found with orbital semimajor axis lengths that place them between the orbits of Mars and Jupiter. For example, Ceres, the largest minor planet in the asteroid belt (also classified as a dwarf planet), can be found between Mars and Jupiter.
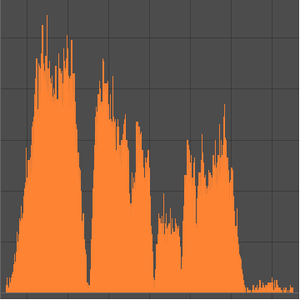
Asteroids that have an orbital resonance with Jupiter (small integer ratio of Jupiter’s orbital period) get disrupted and result in fewer asteroids at those locations. These are easily seen by counting the number of asteroids with a given orbital semimajor axis within the asteroid belt.
First, obtain the semimajor axis of asteroids between 2 and 3.5 AU from the Sun.
Finally, plot the data so you can see the gaps, known as Kirkwood gaps, that result from orbital resonances with Jupiter.
Now annotate the "valleys" where few minor planets are found at a given small integer ratio of the orbital period of Jupiter.
You can make use of a function to compute the semimajor axis of the orbit of an asteroid if you know the ratio between the orbital period of the asteroid and that of Jupiter, using the simplified form of Kepler's third law.
Within the range of interest, you can find all small integer ratios, which should correspond to likely gaps in the asteroid belt. Generate a pair of the orbit period fraction with respect to Jupiter and the corresponding orbital semimajor axis value.
To annotate the preceding original histogram, you need to generate these annotations using text and arrows.
You can now plot the location of orbits with possible orbital resonances with Jupiter. For example, the large dip labeled "3:1" corresponds to minor planets that orbit three times for every one orbit of Jupiter. Most of the small integer ratios correspond to observed dips in the number of asteroids at those distances, due to gravitational perturbations.