Visualize valores próprios de grafos
Valores próprios de grafos podem fornecer informações sobre as propriedades estruturais do grafo.
Gere um grafo direcionado acíclico de um grafo base inicial.
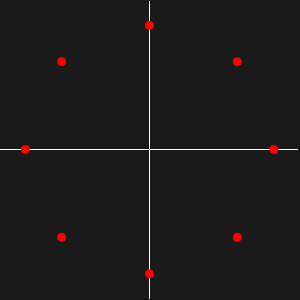
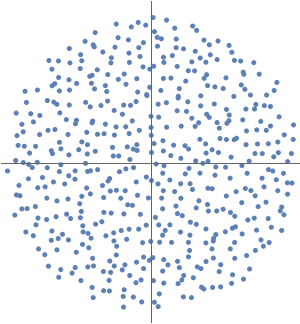
Se um grafo é acíclico, sua matriz de adjacência é nilpotente e todos os seus valores próprios são zero.
Se um grafo é simétrico, sua matriz de adjacência é simétrica e seus valores próprios são reais.
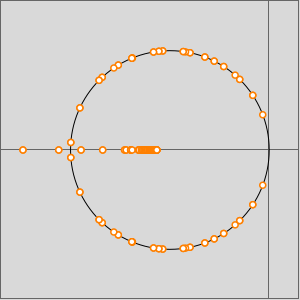
Se um grafo é bipartido, o espectro de sua matriz de adjacência é simétrico rotacionalmente em relação a 0. Ou seja, se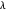 
é um valor próprior da matriz de adjacência, então é 
.
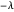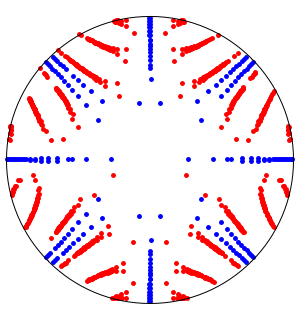
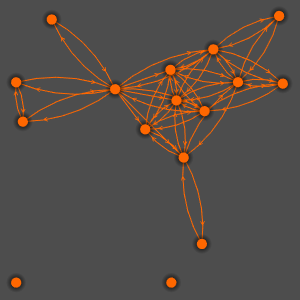
Gere um grafo mostrando um conjunto de símbolos que estão linkados na documentação da Wolfram.
O gráfico dos valores próprios do grafo mostra que os ciclos estão presentes, mas que o grafo não é simétrico nem bipartido.
O gráfico não é simétrico porque ComplexExpand está linkado a Complex, Conjugate, Im e Re, mas não vice-versa.
