Explore Function Spaces
A function space is a set of functions of a given kind from a set 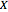 to a set
to a set 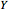 . It is called a space because in many applications, it is a topological space and is often associated with a measure space.
. It is called a space because in many applications, it is a topological space and is often associated with a measure space.
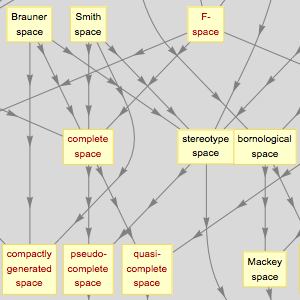
Function spaces tend to involve topological concepts that are very general and abstract. The "FunctionSpace" entity domain encodes properties of more than 125 spaces and makes them available in a form that is as computational as possible.
For example, Lebesgue spaces are defined using a natural generalization of the 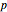 -norm for finite-dimensional vector spaces. A nice summary of the properties of the order-
-norm for finite-dimensional vector spaces. A nice summary of the properties of the order-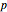 Lebesgue space over
Lebesgue space over 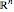 can be obtained directly form a Wolfram|Alpha query, here customized to display only the most significant pods.
can be obtained directly form a Wolfram|Alpha query, here customized to display only the most significant pods.
There are actually many varieties of Lebesgue spaces defined, based on their domain and measure space.
Consider now the special case of the  space, which has the norm defined as follows.
space, which has the norm defined as follows.
Here, the PureMath context is used as a placeholder for mathematical objects that are not (yet?) built into the Wolfram Language.
Information about notable people who studied each space is also available.
For convenience, a tabular display of various notations in use for each space is also provided.
As an illustration of how the information in this entity domain can be used, a few simple computations are performed.
Consider the dual space of  (for
(for  ).
).
Now take the dual of the dual space 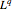 and perform symbolic simplification on the resulting parametrized entity.
and perform symbolic simplification on the resulting parametrized entity.
Since this is equal to the original space, you can see that 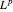 is reflexive, i.e.
is reflexive, i.e. 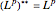 .
.
This can also be computed directly.
More detailed information about spaces is provided via the "TypesetDescription" property, which in the case of a reflexive space gives the following rigorous definition together with some helpful additional description.