関数空間を調べる
関数空間は集合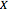 
から集合 
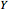の与えられた種類の関数の集合である．これが空間と呼ばれるのは，多くの分野でそれが位相空間であり測度空間と関連していることが多いからである．
関数空間は非常に一般的で抽象的な位相的概念にかかわる傾向がある．"FunctionSpace"実体領域は125を超える空間の特性を符号化し，可能な限り計算的な形式で利用できるようにする．
例えば，ルベーグ(Lebesgue)空間は，有限次元のベクトル空間に対する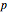 
ノルムの自然な一般化を使って定義される．
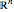上の次数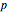 
のルベーグ空間の特性の要約は，Wolfram|Alphaのクエリから直接得ることができる．ここでは最も重要なポッドだけを表示するようカスタマイズしてある．
領域と測度空間に基づいて定義されるルベーグ空間には多数の変形がある．
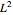空間の特殊なケースを考える．そのノルムは以下のように定義される．
ここで，まだWolfram言語に組み込まれていない数学オブジェクトのプレースホルダとしてPureMathコンテキストが使われる．
それぞれの空間を研究した有名な人々についての情報が利用できる．
簡便性のために，それぞれの空間に対して使われる表記の表形式を提供する．
この実体領域の情報がどのように使われるかの例示として，簡単な計算をいくつか行う．
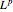（このとき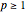 
）の二重空間を考える．
ここで二重空間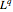 
から両数を取り，結果のパラメータ化された実体で記号簡約化を施す．
これはもとの空間に等しいので，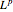
は回帰的，つまり
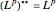であることが分かる．
これは直接計算することもできる．
空間についてのより詳細な情報は，"TypesetDescription"特性で提供される．回帰的空間の場合，この特性は役に立つ追加説明とともに，次のような綿密な定義を与える．
