Exploración de los espacios de funciones
Un espacio de funciones es un conjunto de funciones de un tipo dado de un conjunto  a un conjunto
a un conjunto 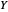 . Se llama espacio porque en muchas aplicaciones, es un espacio topológico y a menudo se asocia con un espacio de medidas.
. Se llama espacio porque en muchas aplicaciones, es un espacio topológico y a menudo se asocia con un espacio de medidas.
Los espacios funcionales tienden a involucrar conceptos topológicos que son muy generales y abstractos. El dominio de la entidad "FunctionSpace" codifica propiedades de más de 125 espacios y los pone a disposición en una forma lo más computacional posible.
Por ejemplo, los espacios de Lebesgue se definen usando una generalización natural de la norma 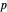 para espacios vectoriales de dimensiones finitas. Puede obtener un buen resumen de las propiedades del espacio de Lebesgue de orden
para espacios vectoriales de dimensiones finitas. Puede obtener un buen resumen de las propiedades del espacio de Lebesgue de orden 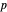 sobre
sobre 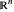 directamente desde una consulta Wolfram|Alpha, aquí personalizada para mostrar solo los pods más significativos.
directamente desde una consulta Wolfram|Alpha, aquí personalizada para mostrar solo los pods más significativos.
En realidad, hay muchas variedades de espacios de Lebesgue definidos, en función de su dominio y espacio de medida.
Considere ahora el caso especial del espacio 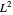 que tiene la norma definida de la siguiente manera.
que tiene la norma definida de la siguiente manera.
Aquí, el contexto PureMath se usa como marcador de posición para objetos matemáticos que (¿aún?) no han sido integrados en Wolfram Language.
También está disponible información sobre personas notables que estudiaron cada espacio.
Para mayor comodidad, también se proporciona una visualización tabular de varias anotaciones en uso para cada espacio.
Como ilustración de cómo se puede usar la información en este dominio de entidad, se realizan algunos cálculos simples.
Considere el espacio dual de 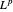 (para
(para 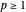 ).
).
Ahora tome el dual del espacio dual 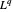 y realice una simplificación simbólica en la entidad parametrizada resultante.
y realice una simplificación simbólica en la entidad parametrizada resultante.
Como esto es igual al espacio original, puede ver que 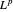 es reflexivo p. ej.
es reflexivo p. ej. 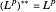 .
.
Esto también se puede calcular directamente.
Se proporciona información más detallada sobre los espacios a través de la propiedad "TypesetDescription", que en el caso de un espacio reflexivo proporciona la siguiente definición rigurosa junto con alguna descripción adicional útil.