Cálculo de densidades de empaques de red
El dominio de la entidad "Lattice" contiene información útil sobre retículos con nombre clásico.
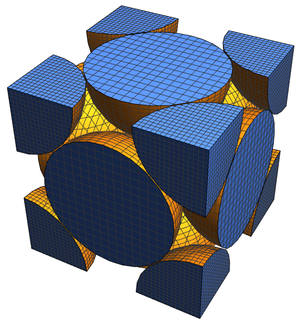
Por ejemplo, considere la red cúbica centrada en el cuerpo (BCC), que puede visualizarse inmediatamente usando la propiedad "Image".
Una propiedad importante de un empaquetamiento reticular es la fracción de espacio ocupado por esferas empaquetadas con la configuración relevante. Para una red BCC, esta densidad de empaquetamiento viene dada por lo siguiente.
En otras palabras, las esferas llenan aproximadamente el 68% del espacio total en el empaque cúbico centrado en el cuerpo.
Los vectores mínimos que generan esta red están disponibles como la propiedad "MinimalVectors".
Teniendo esto en cuenta, puede hacer una visualización que llene el espacio a partir del cual esta densidad se puede calcular directamente. Comience por construir una lista que dé los centros de esferas que aparecen en la celda unitaria a partir de los vectores mínimos.
Ahora restrinja el rango de gráfico a la región de la celda unitaria.
La visualización se puede hacer un poco más elaborada utilizando esferas rellenas en lugar de huecas.
Como se puede ver en este diagrama, hay ocho octavas esferas y una esfera completa en la celda unitaria, contribuyendo 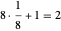 esferas completas. Tomando a como el radio de las esferas, según el teorema de Pitágoras aplicado a una diagonal espacial, el cubo general tiene una longitud de borde
esferas completas. Tomando a como el radio de las esferas, según el teorema de Pitágoras aplicado a una diagonal espacial, el cubo general tiene una longitud de borde 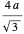 , lo que significa que la densidad de empaquetamiento de las esferas viene dada por la expresión ya vista.
, lo que significa que la densidad de empaquetamiento de las esferas viene dada por la expresión ya vista.
Ahora considere el retículo de fase cúbica centrada (FCC, por sus siglas en inglés).
Este empaque reticular tiene una mayor densidad de empaque.
Es decir, las esferas, por lo tanto, ocupan aproximadamente el 74% del espacio total en el empaque de red de fase cúbica centrada.
Como antes, haga una visualización que llene el espacio al encontrar primero los centros de las esferas en un empaque FCC.
Como se puede ver en este diagrama, hay ocho octavas esferas y seis medias esferas en la celda unitaria, que contribuyen 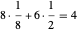 de esferas completas. Tomando
de esferas completas. Tomando 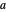 como el radio de las esferas, según el teorema de Pitágoras aplicado a una diagonal de la cara, el cubo total tiene una longitud de borde
como el radio de las esferas, según el teorema de Pitágoras aplicado a una diagonal de la cara, el cubo total tiene una longitud de borde 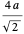 , lo que significa que la densidad de empaque de las esferas viene dada por la expresión ya recuperada.
, lo que significa que la densidad de empaque de las esferas viene dada por la expresión ya recuperada.
El empaque cerrado hexagonal (HCP) es otro empaque estrechamente relacionado.
Tiene la misma densidad de empaque que del reticular de fase cúbica centrada.
Al igual que en el empaquetamiento cúbico compapcto centrado, cada esfera está rodeada por otras 12 esferas en HCP. Tomar la malla Delaunay de los vectores mínimos para este empaque es equivalente a conectar los centros de las 12 esferas externas y permitir que los bordes sean las caras de un poliedro envolvente.
Esto da como resultado el poliedro conocido como ortobicúpula triangular.