Investigación de la hipótesis de Riemann
Publicado por primera vez en un innovador artículo en 1859 por Bernhard Riemann, la hipótesis de Riemann es una hipotesis matemática profunda que establece que la función zeta de Riemann no trivial es cero, es decir, los valores de la función zeta de Riemann
otros que 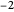 ,
, 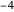 ,
, 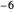 , … tal que
, … tal que 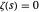 todos se encuentran en la "línea crítica"
todos se encuentran en la "línea crítica" 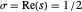 , donde
, donde 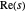 denota la parte real de una variable compleja
denota la parte real de una variable compleja  .
.
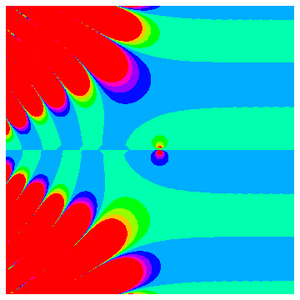
Mientras que la función zeta de Riemann oscila infinitamente a lo largo del eje real negativo, asintóticamente se acerca a 1 a lo largo del eje real positivo.
El comportamiento se vuelve aún más complicado a lo largo de la línea crítica.
De hecho, la trama anterior da una idea más representativa de la verdadera complejidad que surge en el plano complejo.
Los primeros 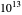 ceros no triviales de la función zeta de Riemann se han probado y se ha encontrado que satisfacen la hipótesis de Riemann. Por lo tanto, es bastante sorprendente que, a pesar de la abundante evidencia numérica y del considerable esfuerzo, nadie haya podido probar esta hipótesis en los últimos 250 años.
ceros no triviales de la función zeta de Riemann se han probado y se ha encontrado que satisfacen la hipótesis de Riemann. Por lo tanto, es bastante sorprendente que, a pesar de la abundante evidencia numérica y del considerable esfuerzo, nadie haya podido probar esta hipótesis en los últimos 250 años.
Se conocen muchos resultados en matemáticas "suponiendo que se cumpla la hipótesis de Riemann". Esto significa que una prueba de la hipótesis de Riemann establecería inmediatamente una multitud de otros resultados en matemáticas. También hay muchas formulaciones alternativas de la hipótesis de Riemann, una colección que el dominio de la entidad RiemannHypothesisFormulation intenta recopilar.
Actualmente el conjunto contiene alrededor de 70 formulaciones.
Estas formulaciones a su vez se pueden agrupar en aproximadamente la mitad de esa cantidad de familias.
La forma original de la hipótesis de Riemann se puede establecer usando la aritmética cuantificadora en la siguiente forma concisa.
Si bien, en principio, esta es una expresión computable, ya que nadie sabe cómo establecer la hipótesis de Riemann, aplicar la eliminación del cuantificador no se evalúa (después de todo, si Mathematica pudiera resolver los cuantificadores en este caso, sería capaz de establecer la validez de La hipótesis de Riemann).
Ahora examine los tipos de formulaciones alternativas presentes en el dominio RiemannHypothesisFormulation.
Quizás la declaración alternativa más famosa de la hipótesis de Riemann se refiere a la positividad de las expresiones dadas por derivados de la función 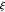 , una función estrechamente relacionada con
, una función estrechamente relacionada con 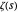 ; es la desigualdad de Li. Esta formulación, conocida como la desigualdad de Li, puede expresarse formalmente de la siguiente manera.
; es la desigualdad de Li. Esta formulación, conocida como la desigualdad de Li, puede expresarse formalmente de la siguiente manera.
Wolfram Language puede calcular directamente formas cerradas para la expresión dentro de la desigualdad (aunque hacerlo para índices grandes requiere el uso de relaciones de recurrencia conocidas, satisfechas por las derivadas de 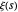 ). Para comenzar, primero extraiga la desigualdad de la formulación.
). Para comenzar, primero extraiga la desigualdad de la formulación.
Ahora defina las constantes 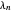 de Li, cuya positividad para todos los
de Li, cuya positividad para todos los 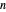 positivos es equivalente a la hipótesis de Riemann.
positivos es equivalente a la hipótesis de Riemann.
Calcular exactamente y numerar las constantes hasta el orden cinco verifica que sean realmente positivas.
Por supuesto, la desigualdad de Li es solo una formulación alternativa. Varios matemáticos han derivado múltiples formulaciones para la hipótesis de Riemann. Aquí hay una lista de formuladores ordenados por el número de formulaciones distintas representadas en la colección.
Ahora puede construir una línea de tiempo de investigadores que ilustre hasta cierto punto el alto nivel de actividad que se ha dedicado a la hermosa pero obstinada hipótesis de Riemann.