충전된 삼각형 시트 장세기 모델링하기
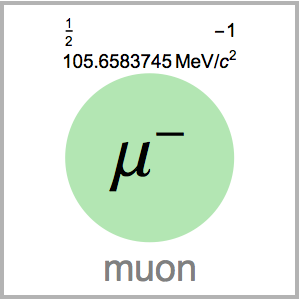
Wolfram 언어는 강력한 계산 언어이며, 사람들 사이의 과학적인 커뮤니케이션을 위한 효율적인 언어입니다. 이를 보여주는 좋은 예로 물리계의 실체 영역을 들 수 있습니다. "PhysicalSystem"에서 이용할 수 있는 범위를 알기 위해 사용 가능한 실체의 예를 살펴봅니다.
물리계는 실체 클래스로 분류되어 있기 때문에 관심 있는 물리계를 쉽게 찾을 수 있습니다. 현재 27개의 중복된 실체 클래스가 있습니다. 그 일부를 다음에서 알아봅니다.
물리계 영역은 "Country" 영역 등과 같이 주로 숫자나 텍스트의 데이터를 포함하는 것이 아니라 교과서에 있는 것과 같은 수식을 주로 포함하고 있습니다. 이들을 어떻게 사용할 수 있는지를 보기 위하여 관심있는 계를 충전된 삼각 시트로 살펴봅니다.
"NonMissingProperties"를 호출하면 이 실체에 무엇을 사용할 수 있는지 쉽게 알 수 있습니다.
일반적으로 "PhysicalSystem" 영역의 실체는 시스템의 전반적인 물리 매개 변수를 설명하는 "시스템 변수"의 집합과 연관됩니다. 공간의 충전된 삼각 시트는 이러한 시트의 전하 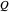 와
와 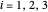 일 때의 정점
일 때의 정점 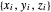 의 좌표입니다.
의 좌표입니다.
지정된 특성은 이러한 계의 변수에 의존할 가능성도 계의 일반화된 좌표에 의존할 가능성도 있습니다. 예를 들어, 전하 밀도를 살펴봅니다.
"PhysicalSystem"에 의해 반환되는 수식에서 흔히 있는 일이지만, 이 식의 머리는 Inactive[ReplaceRepeated]입니다. 이에 따라 식을 짧고 또한 이해하기 쉽게하는 중간 변수를 사용할 수 있게됩니다. 예를 들어, 위에 제시된 식에서 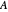 는 삼각형의 면적,
는 삼각형의 면적, 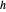 는 삼각형에서 측정점까지의 수직 거리를 나타냅니다. DiracDelta와 Piecewise는 전하 밀도 (무한히 얇은)가 삼각 시트에서만 0이 아님을 나타냅니다. 대체를 활성화하면 식은 계의 변수와 일반화된 좌표만을 포함하는 식으로 간략화 됩니다.
는 삼각형에서 측정점까지의 수직 거리를 나타냅니다. DiracDelta와 Piecewise는 전하 밀도 (무한히 얇은)가 삼각 시트에서만 0이 아님을 나타냅니다. 대체를 활성화하면 식은 계의 변수와 일반화된 좌표만을 포함하는 식으로 간략화 됩니다.
더 재미있는 특성은 대전된 시트의 전기장을 들 수 있습니다. 단순화된 시각화를 위해 2 차원 시트를 생각해봅니다(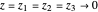 을 취합니다). 장의 형식은 다음의 EntityValue의 호출에서 찾을 수 있습니다(결과가 커지기 때문에 여기에서는 표시하지 않습니다).
을 취합니다). 장의 형식은 다음의 EntityValue의 호출에서 찾을 수 있습니다(결과가 커지기 때문에 여기에서는 표시하지 않습니다).
관심있는 삼각형을 선택하여 그 정점 좌표를 fieldForm으로 대체하고 활성화하면 전기장 벡터에 대한 간단한 (복소수에서도) 닫힘 식의 해를 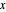 -
-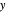 평면의 좌표 함수로 얻을 수 있습니다.
평면의 좌표 함수로 얻을 수 있습니다.
위의 식은 매우 복잡하기 때문에 쉽게 표시 하기 위해 TraditionalForm Pane으로 렌더합니다.
마지막 단계로, 이러한 수식에서 흐르는 장세기를 시각화 해봅니다. 다행히도, Wolfram 언어에는 이를 위한 함수 StreamDensityPlot이 포함되어 있습니다. 플롯하기 전에 위의 식의 QuantityVariable의 항목을 주의하여 제거해야 하며, 이를 행하기 위한 대체를 아래에서 설명합니다. 또한 더 재미있는 플롯을 만드는 데 대전된 삼각형을 두 개 중첩하여 그 상대적인 위치, 각도, 전하의 변화에 따라 그들이 어떻게 상호 작용 하는지를 나타내는 Manipulate를 구축합니다. 코드와 결과의 애니메이션을 보여주기 때문에, Wolfram 언어로 물리계의 시뮬레이션을 실제로 실행 해 보길 권장합니다.