Convex Polygons & Properties
Version 12 adds convex optimization and opens up many applications in classes of problems that can be identified to be convex in geometry.
Find the inequality representation for a convex polygon using LinearOptimization.
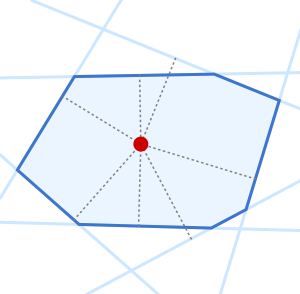
The analytic center of a convex polygon can be defined as a point inside the polygon that maximizes the product of distances to the sides. The distance of a point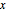 
in the polygon to each side is 
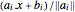, and so the analytic center is 
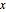that maximizes 
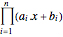. To express the problem as a convex minimization, take 
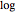and negate the objective 
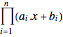. The transformed objective is 
.
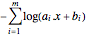Visualize the location of the analytic center.
