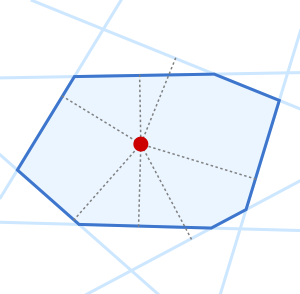
凸多角形と特性

バージョン12には凸最適化が加えられ、幾何で凸であると特定できる問題のクラスにおいて数多くの応用が可能となった．

LinearOptimizationを使って，凸多角形の不等式表現を求める．

凸多角形の解析中心は，辺までの距離の積を最大化する，多角形内の点として定義することができる．多角形の点 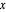の各辺までの距離は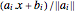，であり，解析中心は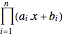，を最大化する 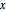である．問題を凸最小化として表現するためには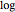，を取り，対象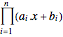をネゲートする．変換された対象は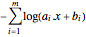である．

解析中心の位置を可視化する．