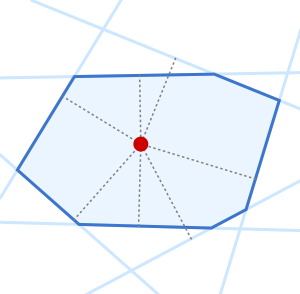
Polygones et propriétés convexes
La version 12 ajoute l'optimisation convexe et permet ainsi d'accéder à de nombreuses applications dans des classes de problèmes qui peuvent être identifiées comme convexes en géométrie.
Recherchez la représentation de l'inégalité pour un polygone convexe en utilisant LinearOptimization.
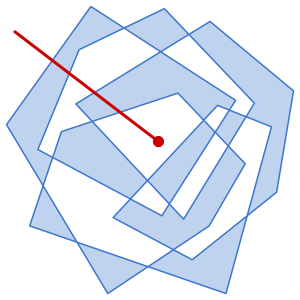
Le centre analytique d'un polygone convexe peut être défini comme un point à l'intérieur du polygone qui maximise le produit des distances aux côtés. La distance de chaque côté d'un point 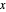 dans le polygone correspond à
dans le polygone correspond à 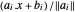 , donc le centre analytique correspond à
, donc le centre analytique correspond à 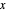 et maximise
et maximise 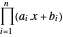 . Pour exprimer le problème en tant que minimisation convexe, prenez
. Pour exprimer le problème en tant que minimisation convexe, prenez 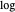 et soustrayez l'objectif
et soustrayez l'objectif 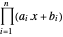 . L'objectif transformé correspond à
. L'objectif transformé correspond à 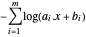 .
.
Visualisez l'emplacement du centre analytique.