Wenn das Mittel nichts bringt – robuste Lagemaße
Bei Heavy-tailed-Verteilungen wie der Cauchy- oder Pareto-Verteilung handelt es sich um Verteilungen, auf deren Rändern (tails) mehr Masse oder Gewicht liegt als beispielsweise bei der Exponentialverteilung. Das bedeutet, dass selten auftretende Ereignisse eine nicht unerhebliche Wahrscheinlichkeit haben. Solche Verteilungen weisen häufig undefinierte Momente, beispielsweise Mittelwerte, auf. Sie können das winsorisierte oder getrimmte Mittel berechnen, um das Zentrum der Stichprobe zu bestimmen.
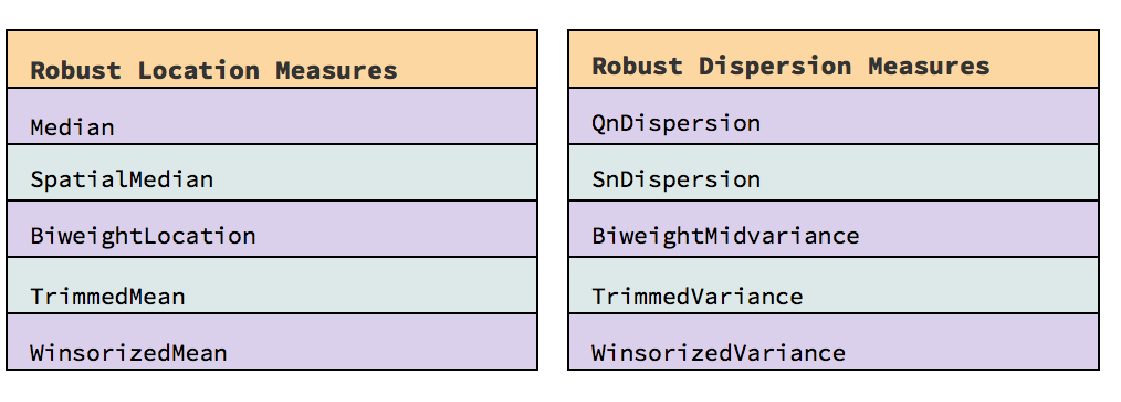
Robuste Verfahren für Lagemaße und Streuungsmaße einer Stichprobe in Version 12:
Werfen Sie einen Blick auf eine Heavy-tailed-Verteilung.
Der Mittelwert ist unbestimmt.
Es handelt sich um eine Heavy-tailed-Verteilung und der Großteil der Masse befindet sich in den Rändern. Berechnen Sie die Quartile.
Berechnen Sie den Mittelwert nach Entfernen von 10 % des langen Schwanzes.
Dieser Vorgang wird auch als Stutzen oder Trimmen der Verteilung bezeichnet.
Berechnen Sie den 10-%-winsorisierten Mittelwert.
Da nicht alle Werte der Verteilung berücksichtigt werden, arbeitet man mit sogenannten zensierten Daten.
Der Unterschied zwischen dem Verwerfen von 10 % der größten Werte und dem Abschneiden einer gleichen Anzahl von Werten am Anfang und am Ende der Folge ist signifikant, was den endlastigen Charakter dieser Verteilung ausmacht.