Full Access to System Equations
Extracting equations and processing them for in-depth analysis and design is a powerful tool for many workflows. In this example, a discrete controller for a continuously stirred tank reactor (CSTR) is designed by discretizing its equations.
Find an optimal control signal for a CSTR. The temperature in the tank influences a reaction rate, while the temperature in the cooling jacket acts as a control signal. The goal is to go from one concentration to another as quickly as possible while obeying safety limitations in temperature.
Get the system equations.
Replace the parameters with their numerical values. Variables obtained are quantity variables. Convert them into regular variables for further processing.
Define different parameters used in your calculation. First, define parameters for the step size in the numerical differentiation.
Give initial and target values for the temperature in the cooling jacket, the temperature in the tank and the concentration.
Replace the derivatives with forward differences.
Define the cost function that you want to minimize.
Create constraints for the temperatures, requiring them to stay inside given safety limits. Also, create constraints by discretizing into steps and applying logic operations for each step.
Define and apply the initial conditions.
Find the optimal control signal.
Collect the results in three signal variables.
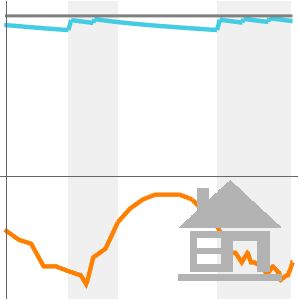
Show the results in three plots.