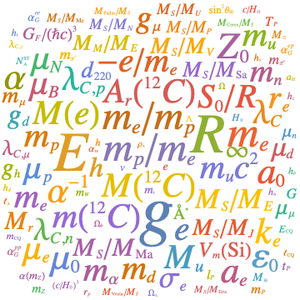Unsicherheit in Naturkonstanten
Der Entitätenbereich "PhysicalConstant" enthält eine umfangreiche Tabellierung der physikalischen Konstanten, darunter viele grundlegende Konstanten der Natur.
Eine umfassende Bandbreite von Eigenschaften steht auch für physikalische Konstanten zur Verfügung.
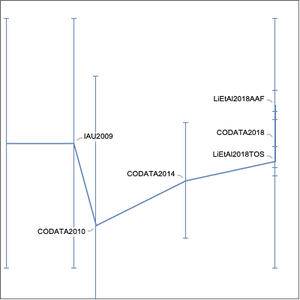
Zentrales Element dieser Eigenschaften sind der beste Messwert und Unsicherheit. Dieses Beispiel zeigt, dass verschiedene Naturkonstanten unterschiedliche Unischerheiten aufweisen.
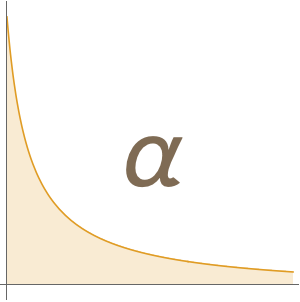
Betrachten wir die Gravitationskonstante  , die im Gesetz der universellen Gravitation vorkommt.
, die im Gesetz der universellen Gravitation vorkommt.
Hier ist eine Liste des besten aktuellen Wertes mit der dazugehörigen Unsicherheit.
Um die Berechnung zu erleichtern, kann der Wert einer Konstanten mit Unsicherheit zurückgegeben werden, die in einer Reihe von verschiedenen Formen enthalten ist, wie unten für  dargestellt.
dargestellt.
Um die relativen Unsicherheiten von physikalischen Konstanten zu untersuchen, rufen Sie zunächst die Werte für alle Konstanten ab, entfernen Sie dann Konstanten mit genauen Werten, unbekannte Unsicherheiten und die Atom- und Naturkonstanten.
Erstellen Sie eine neue Datenliste, in denen relative Unsicherheiten in präzise Werte umgewandelt werden. Heben Sie auch einige wichtige Konstanten hervor, um sicherzustellen, dass sie im Ergebnisdiagramm mit der OptionLabelVisibility markiert sind.
Plotten Sie nun die sortierten Genauigkeiten der tabellarischen Konstanten.
Dieser Plot zeigt sofort die enormen Unterschiede in der Genauigkeit, mit der verschiedene Konstanten bekannt sind. So ist beispielsweise die Gravitationskonstante die am wenigsten mit Sicherheit bekannte Konstante aus der Kernmenge der fundamentalen Naturkonstanten (die vierte Stelle nach dem Komma ist bereits unsicher), während der  -Faktor erst nach der zwölften Stelle nach dem Komma unsicher ist.
-Faktor erst nach der zwölften Stelle nach dem Komma unsicher ist.
Die Genauigkeit, mit der physikalische Konstanten bekannt sind, kann auch gut als Wortwolke betrachtet werden, in der Symbole mit einer Größe dargestellt werden, die mit der Genauigkeit gewichtet wird, mit der sie bekannt sind (und in der die Genauigkeit durch Kubieren skaliert wurde, um die Variationen besser hervorzuheben).