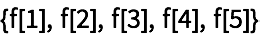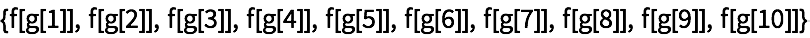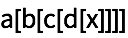An Elementary Introduction to the Wolfram Language
25Maneras de aplicar funciones
f[x] significa “aplicar la función f a x”. En Wolfram Language, una forma alternativa de escribir lo mismo es f@x.
f@x es lo mismo que f[x]:
In[1]:=
Click for copyable input
Out[1]=
A menudo resulta conveniente usar @ para escribir funciones en cadena:
In[2]:=
Click for copyable input
Out[2]=
El código puede resultar más fácil de leer evitando el uso de los corchetes, si se escribe:
In[3]:=
Click for copyable input
Out[3]=
Otra forma más de escribir f[x] en Wolfram Language es: como una “coletilla”, en la forma x//f.
Aplique f “como coletilla” a x:
In[4]:=
Click for copyable input
Out[4]=
Puede tenerse una sucesión de “coletillas”:
In[5]:=
Click for copyable input
Out[5]=
Aquí las funciones se leen en el orden en que se van aplicando:
In[6]:=
Click for copyable input
Out[6]=
Una forma muy común de usar // es en la aplicación de N (para fines de evaluación numérica) “como coletilla”.
Aplique la evaluación numérica “como coletilla”:
In[7]:=
Click for copyable input
Out[7]=
A medida que se va trabajando con Wolfram Language, se acaba por usar todo el tiempo una notación muy poderosa, a saber, /@, que significa “aplicar a cada elemento”.
Aplique f a cada elemento de una lista:
In[8]:=
Click for copyable input
Out[8]=
Normalmente, f se aplicaría a la lista misma:
In[9]:=
Click for copyable input
Out[9]=
Framed es una función que muestra un marco alrededor de algo.
Muestre x con un marco:
In[10]:=
Click for copyable input
Out[10]=
Si se aplica Framed a una lista, simplemente se muestra enmarcada la lista completa.
Aplique Framed a una lista completa:
In[11]:=
Click for copyable input
Out[11]=
@ hace exactamente lo mismo:
In[12]:=
Click for copyable input
Out[12]=
Ahora se usa /@ para aplicar Framed a cada elemento de la lista:
In[13]:=
Click for copyable input
Out[13]=
Esto trabaja de igual forma con cualquier otra función. Por ejemplo, aplicar la función Hue separadamente a cada número de una lista.
/@ aplica Hue separadamente a cada número en la lista:
In[14]:=
Click for copyable input
Out[14]=
Esto es lo que hace la /@:
In[15]:=
Click for copyable input
Out[15]=
Lo mismo pasa con Range, aunque ahora la salida es una lista de listas.
/@ aplica separadamente Range a cada número, dando como resultado una lista de listas:
In[16]:=
Click for copyable input
Out[16]=
Aquí se ve la equivalencia, al escribir todo en detalle:
In[17]:=
Click for copyable input
Out[17]=
Si ahora se tiene una lista de listas, /@ es lo que se necesitaría para efectuar una operación por separado en cada una de las sublistas.
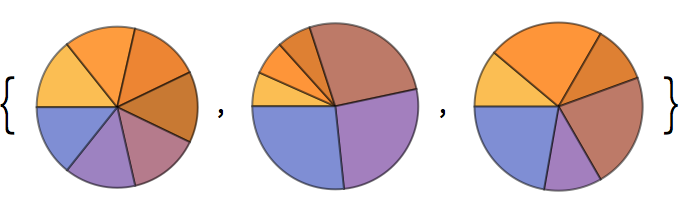
Aplique PieChart separadamente a cada una de las listas en una lista de listas:
In[18]:=
Click for copyable input
Out[18]=
La misma idea puede extenderse exactamente a muchas otras funciones.
Aplique Length a cada elemento, para producir la longitud de cada sublista:
In[19]:=
Click for copyable input
Out[19]=
La aplicación de Length a la lista completa simplemente daría el número total de sublistas:
In[20]:=
Click for copyable input
Out[20]=
Aplique Reverse a cada elemento, para producir tres listas diferentes, en orden inverso:
In[21]:=
Click for copyable input
Out[21]=
La aplicación de Reverse a la lista completa pondría sus elementos en orden inverso:
In[22]:=
Click for copyable input
Out[22]=
Como siempre, el uso de corchetes es exactamente equivalente:
In[23]:=
Click for copyable input
Out[23]=
Algunas de las funciones que realizan cálculos son listables, lo que significa que de manera automática se aplican a los elementos de una lista.
N es listable, así que no es necesario el uso de /@ para que se aplique a cada uno de los elementos de una lista:
In[24]:=
Click for copyable input
Out[24]=
Lo mismo ocurre con Prime:
In[25]:=
Click for copyable input
Out[25]=
Una función tal como Graphics decididamente no es listable.
Esto produce un sol gráfico con tres objetos:
In[26]:=
Click for copyable input
Out[26]=
Esto produce tres gráficos separados, donde Graphics ha sido aplicada a cada objeto:
In[27]:=
Click for copyable input
Out[27]=
Al escribir f/@{1,2,3}, Wolfram Language lo interpreta como Map[f,{1,2,3}]. f/@x se lee usualmente como “mapear f sobre x”.
Interpretación interna de f/@{1, 2, 3}:
In[28]:=
Click for copyable input
Out[28]=
Vocabulario
f@x equivalente a f[x]
x//f equivalente a f[x]
f/@{a,b,c} aplica f por separado a cada elemento de la lista
Map[f,{a,b,c}] forma alternativa de /@
Framed[expr] enmarca algo
25.1Use /@ y Range para reproducir el resultado de Table[f[n], {n, 5}]. »
Salida esperada:
Out[]=
25.2Use /@ dos veces para generar Table[f[g[n]], {n, 10}]. »
Salida esperada:
Out[]=
25.3Use // para crear a[b[c[d[x]]]]. »
Salida esperada:
Out[]=
Salida esperada:
Out[]=
Salida esperada:
Out[]=
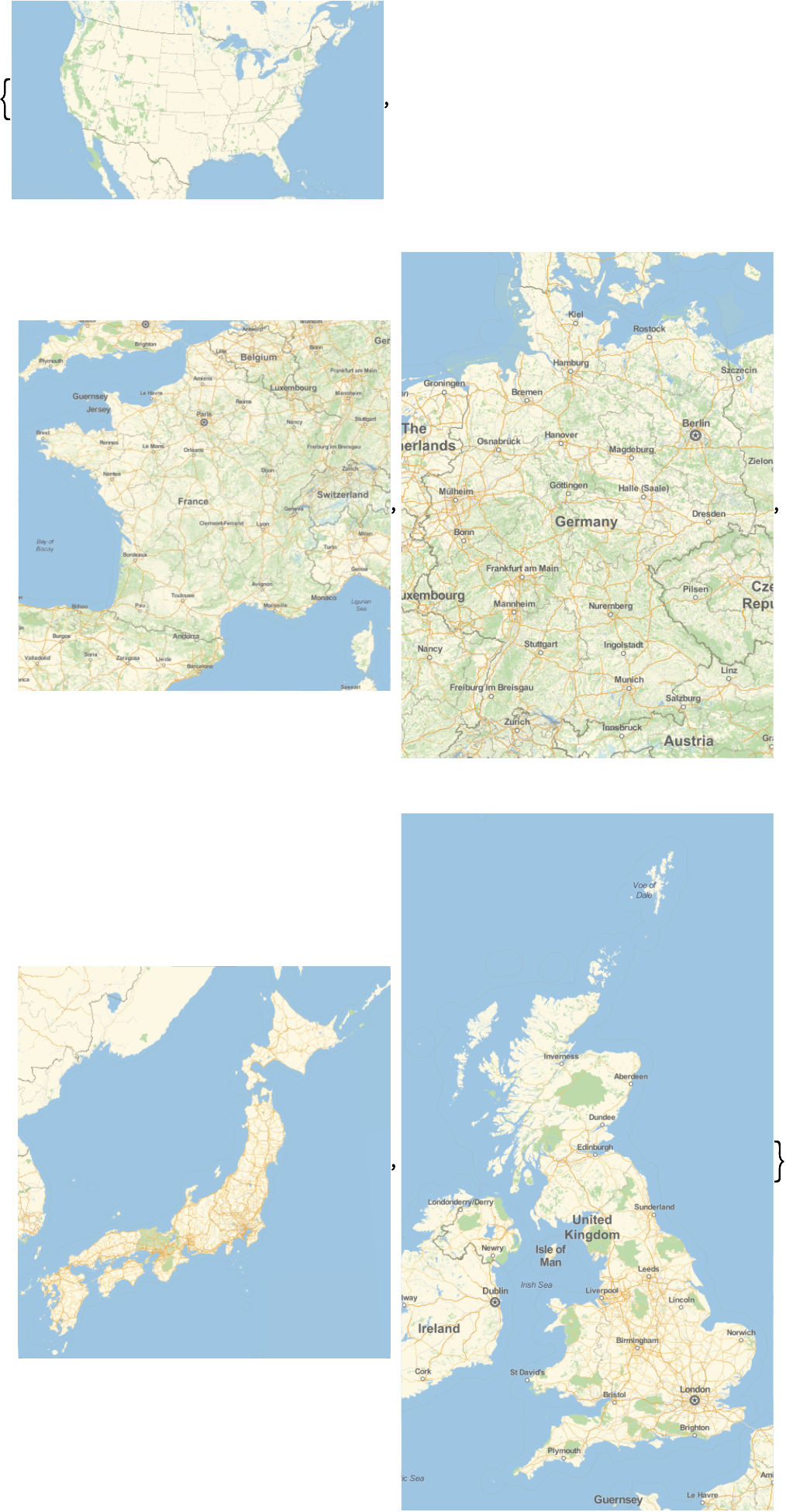
25.6Use /@ para dibujar mapas separados de cada uno de los países en el G5. »
Salida esperada:
Out[]=
25.7Binarice cada una de las banderas de Europa y haga un collage con el resultado. »
Salida esperada:
Out[]=
25.8Haga una lista de los colores dominantes en las imágenes de los planetas, poniendo en una columna los resultados para cada planeta. »
Salida esperada:
Out[]=
25.9Encuentre el total de los números de letra dados por LetterNumber para las letras de la palabra “wolfram”. »
Salida esperada:
Out[]=
Preguntas y respuestas
¿Por qué no usar siempre f@x en vez de f[x]?
f@x es un buen equivalente de f[x], pero el equivalente de f[1+1] es f@(1+1), y en este caso, f[1+1] es más corto y fácil de entender.
¿Por qué /@ se llama Map?
Esto proviene de las matemáticas. Dado un conjunto {1, 2, 3}, f/@{1, 2, 3} puede verse como el mapeo de dicho conjunto en otro.
¿Cómo se dice "//" y "/@"?
Típicamente, “diagonal diagonal” y “diagonal arroba”.
¿Cuándo hay que usar paréntesis con @, // y /@?
Esto está determinado por la precedencia o agrupamiento de operadores diferentes. @ agrupa con mayor fuerza que +, así que f@1+1 significa f[1]+1 y no f@(1+1) o f[1+1]. // agrupa con menos fuerza que +, así que 1/2+1/3//N significa (1/2+1/3)//N. En un cuaderno puede verse cómo están agrupadas las cosas haciendo clic repetidamente en la entrada y observando cómo se expande la selección.
Notas técnicas
Para explorar más
Guía para la programación funcional en Wolfram Language »
 
Download Notebook Version
en