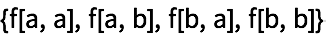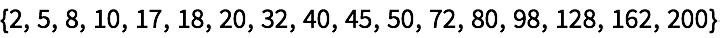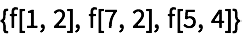Expresiones y su estructura: Una introducción elemental a Wolfram Language

33	Expresiones y su estructura

Se ha visto ya una gran diversidad del material contenido en Wolfram Language: listas, gráficos, funciones puras y muchas cosas más. Se está ahora en posición de comenzar a tratar con una cuestión fundamental en Wolfram Language: el hecho de que cada una de esas cosas —y, de hecho, todo aquello con lo que trata el lenguaje— está construida siempre en la misma forma básica. Todo ello es lo que se llama una expresión simbólica.

Las expresiones simbólicas son una manera muy general de representar una estructura, potencialmente con un significado asociado a esa estructura. f[x,y] es un ejemplo sencillo de expresión simbólica. Por sí misma, esta expresión simbólica no tiene asociado ningún significado en particular de modo que, al escribirla, Wolfram Language la regresará tal cual, sin cambios.

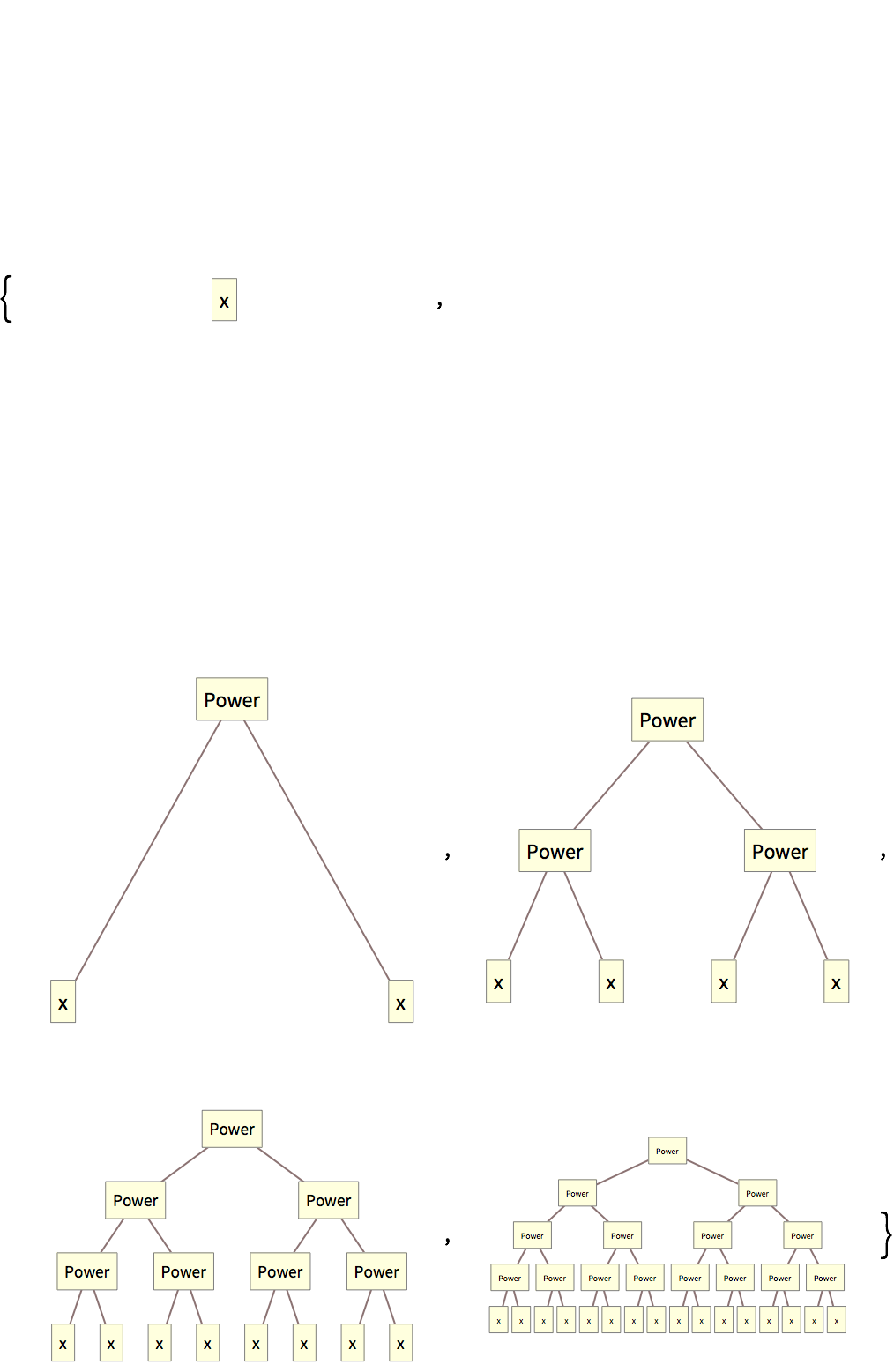
f[x, y] es una expresión simbólica sin ningún significado particular asociado:

In[1]:=

Out[1]=

{x,y,z} es otra expresión simbólica. Aunque internamente es List[x,y,z], se visualiza como {x,y,z}.

La expresión simbólica List[x, y, z] se visualiza como {x, y, z}:

In[2]:=

Out[2]=

Frecuentemente, las expresiones simbólicas están anidadas:

In[3]:=

Out[3]=

FullForm muestra la forma interna de cualquier expresión simbólica.

In[4]:=

Out[4]//FullForm=

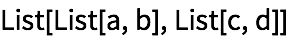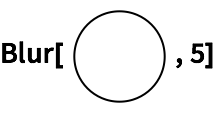
Graphics[Circle[{0,0}]] es otra expresión simbólica, que se muestra en pantalla como la imagen de un círculo. FullForm muestra su estructura interna.

Esta expresión simbólica se visualiza como un círculo:

In[5]:=

Out[5]=

FullForm muestra la estructura subyacente de esa expresión simbólica:

In[6]:=

Out[6]//FullForm=

A menudo sucede que las expresiones simbólicas no solo se muestran en pantalla de una manera especial, sino que, además, se evalúan y producen resultados.

Una expresión simbólica que se evalúa para producir un resultado:

In[7]:=

Out[7]=

Los elementos de la lista se evalúan, pero la lista misma sigue siendo simbólica:

In[8]:=

Out[8]=

He aquí la estructura de la lista como expresión simbólica:

In[9]:=

Out[9]//FullForm=

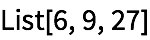Esto es una expresión simbólica que, además, se evalúa:

In[10]:=

Out[10]=

Lo anterior podría escribirse de este modo:

In[11]:=

Out[11]=

¿Cuáles son los elementos constitutivos más elementales en las expresiones simbólicas? Se les llama átomos (por analogía con los elementos constitutivos básicos de los materiales físicos). Los principales tipos de átomos son los números, las cadenas de caracteres y los símbolos.

Por ejemplo, x, y, f, Plus, Graphics y Table, son símbolos. Todo símbolo tiene un nombre único. En ocasiones, también lleva asociado un significado. A veces, también estará asociado con una evaluación. Y también puede ser parte de la definición de una estructura que usarán otras funciones. Pero no es necesario que sea nada de eso; simplemente debe tener un nombre.

Una característica crucial de Wolfram Language es que puede manejar símbolos puramente como tales, como símbolos (“simbólicamente”), sin que se tengan que evaluar, para producir números, por ejemplo.

En Wolfram Language, x puede simplemente ser x, sin que tenga que evaluarse como alguna otra cosa:

In[12]:=

Out[12]=

x no se evalúa, pero la suma se hace de todos modos, según las leyes del álgebra, en este caso:

In[13]:=

Out[13]=

Dados símbolos tales como x, y y f, se puede construir una infinidad de expresiones con ellos. Así, f[x], y f[y], y f[x,y]. Y también f[f[x]] o f[x,f[x,y]], o, para el caso, x[x][y,f[x]] o lo que sea.

En general, toda expresión corresponde a un árbol, cuyas “hojas” últimas son átomos. Una expresión puede mostrarse en forma de árbol usando TreeForm.

Una expresión exhibida en forma de árbol:

In[14]:=

Out[14]//TreeForm=

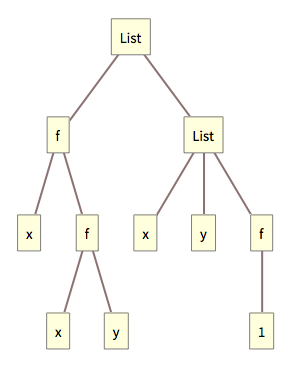Aquí se tiene una expresión sobre gráficos mostrada en forma de árbol:

In[15]:=

Out[15]//TreeForm=

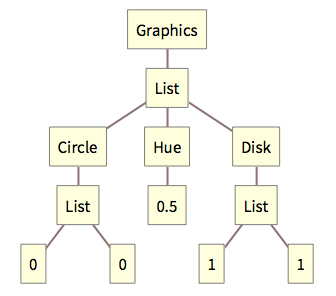A fin de cuentas, las expresiones tienen una estructura muy uniforme, así que las operaciones en Wolfram Language operan sobre ellas también de manera muy uniforme.

Por ejemplo, cualquier expresión tiene partes, como las de una lista, que se pueden extraer mediante el uso de [[...]].

Esto es equivalente a {x, y, z}[[2]], y extrae el segundo elemento de una lista:

In[16]:=

Out[16]=

La extracción de partes funciona de igual forma en la siguiente expresión:

In[17]:=

Out[17]=

Esto extrae el círculo del gráfico:

In[18]:=

Out[18]=

Y, de igual modo, se extraen a continuación las coordenadas de su centro:

In[19]:=

Out[19]=

Esto llega exactamente al mismo resultado:

In[20]:=

Out[20]=

En f[x,y], a f se le llama encabezado de la expresión. x y y se llaman argumentos. La función Head extrae el encabezado de una expresión.

El encabezado de una lista es List:

In[21]:=

Out[21]=

Toda parte de una expresión tiene un encabezado, incluyendo sus átomos.

El encabezado de un entero es Integer:

In[22]:=

Out[22]=

El encabezado de un número real aproximado es Real:

In[23]:=

Out[23]=

El encabezado de una cadena de caracteres es String:

In[24]:=

Out[24]=

Hasta los símbolos tienen un encabezado, a saber: Symbol.

In[25]:=

Out[25]=

Mediante el uso de los patrones se pueden buscar coincidencias de expresiones con encabezados dados. _Integer representa cualquier entero, _String cualquier cadena de caracteres y así sucesivamente.

_Integer es un patrón que coincide únicamente con objetos que tengan el encabezado Integer:

In[26]:=

Out[26]=

Los patrones denominados pueden también tener encabezados especificados:

In[27]:=

Out[27]=

Al usar Wolfram Language, la mayor parte de los encabezados que se ven son símbolos. Sin embargo, hay casos importantes donde aparecen encabezados más complicados. Uno de estos casos es el de las funciones puras, donde al aplicar una función pura dicha función pura aparece como encabezado.

He aquí la forma completa de una función pura (# es Slot[1]):

In[28]:=

Out[28]//FullForm=

Al aplicar la función pura, esta aparece como encabezado:

In[29]:=

Out[29]=

A medida que uno se vuelve más sofisticado en la programación en Wolfram Language, se van encontrando cada vez más casos de encabezados complicados. De hecho, muchas de las funciones que se han revisado hasta ahora tienen formas de operador, donde aparecen como encabezados; y, el usarlas de esta forma, lleva a estilos de programación muy poderosos y elegantes.

Select aparece aquí como encabezado:

In[30]:=

Out[30]=

Tanto Cases como Select aparecen como encabezados en este ejemplo:

In[31]:=

Out[31]=

Todas las operaciones estructurales básicas para listas que se han visto trabajan exactamente igual en el caso de expresiones arbitrarias.

Length no pone atención en cuál sea el encabezado de una expresión; simplemente cuenta los argumentos:

In[32]:=

Out[32]=

/@ tampoco pone atención en cuál sea el encabezado de una expresión; simplemente aplica una función a sus argumentos:

In[33]:=

Out[33]=

Dado que hay muchas funciones que generan listas, resulta conveniente construir estructuras en forma de listas, aun si al final hay que sustituir las listas por otras funciones.

@@ sustituye el encabezado de la lista por f:

In[34]:=

Out[34]=

Esto da Plus[1, 1, 1, 1], lo que entonces se evalúa:

In[35]:=

Out[35]=

Esto convierte una lista en una regla:

In[36]:=

Out[36]=

Aquí se ve una alternativa más sencilla, sin hacer explícita la función pura:

In[37]:=

Out[37]=

Una situación insospechadamente común se da cuando se tiene una lista de listas, donde se quiere sustituir las listas interiores por alguna función. Eso puede efectuarse con @@ y /@. Sin embargo, @@@ es una forma directa y más conveniente para ese propósito.

Sustituya las listas interiores por f:

In[38]:=

Out[38]=

Convierta en reglas las listas interiores:

In[39]:=

Out[39]=

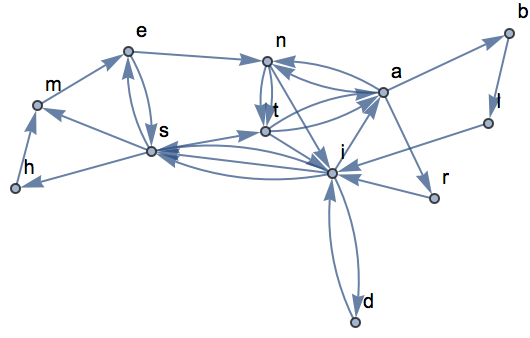
He aquí un ejemplo de cómo se puede utilizar @@@ para construir un grafo a partir de una lista de parejas.

Esto genera una lista de parejas de caracteres:

In[40]:=

Out[40]=

Convierta lo anterior en una lista de reglas:

In[41]:=

Out[41]=

Forme un gráfico de transiciones que muestre cómo cada letra es la sucesiva de cada otra:

In[42]:=

Out[42]=

Vocabulario

FullForm[expr]		muestra la forma interna completa
TreeForm[expr]		muestra la estructura de árbol
Head[expr]		extrae el encabezado de una expresión
_encabezado		busca la coincidencia de una expresión con un encabezado particular
f@@lista		sustituye el encabezado de lista con f
f@@@{lista₁,lista₂, ...}		sustituye los encabezados de lista₁, lista₂, ... con f