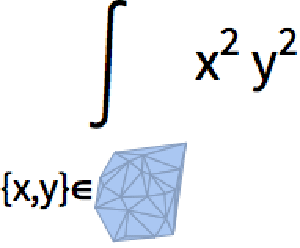Measures
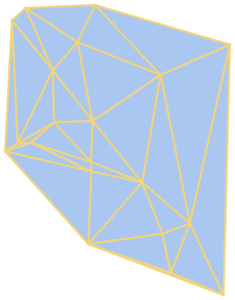
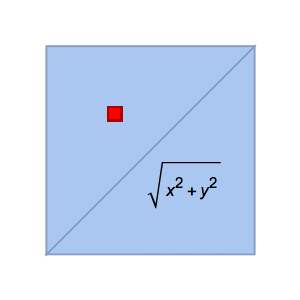
Compute the arc length of a 1D mesh, the area of a 2D mesh, or the volume of a 3D mesh.
| In[1]:= |  X |
| In[2]:= | X |
| Out[2]= |  |
Compute the centroid of any mesh.
| In[3]:= |  X |
| Out[3]= |  |
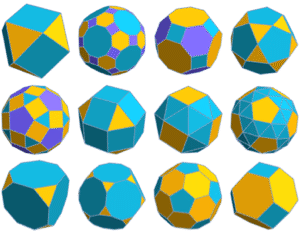
Compute the volume of different levels of a procedurally generated mesh.
| In[5]:= | 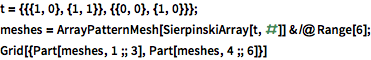 X |
| Out[5]= |  |
| In[6]:= | X |
| Out[6]= |
Find a function that describes the sequence of volumes.
| In[7]:= | X |
| Out[7]= |