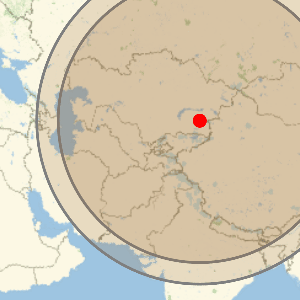
找出美国最内部的点 

Interior Point

获取沿美国边境的 {latitude, longitude} 坐标列表.

In[1]:=

X polygon = Entity["Country", "UnitedStates"]["Polygon"]; coordinates = polygon[[1, 1, 1]];

计算连贯点间的英里距离并进行累加.

In[2]:=

X distances = MapThread[GeoDistance, {coordinates, RotateLeft[coordinates]}]; accumulateddistances = Accumulate[QuantityMagnitude[distances]];

In[3]:=

X ListPlot[accumulateddistances]

Out[3]=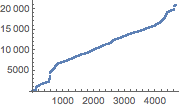

以上为估计的边境的总英里长度.

In[4]:=

X first = First[accumulateddistances]; last = Last[accumulateddistances]

Out[4]=

构建边境的参数化.

In[5]:=

X f = Interpolation[Transpose[{accumulateddistances, coordinates}], InterpolationOrder -> 0]

Out[5]=

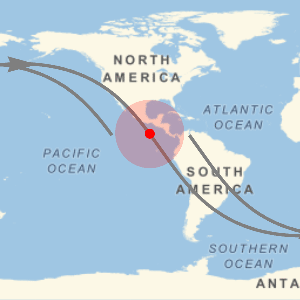
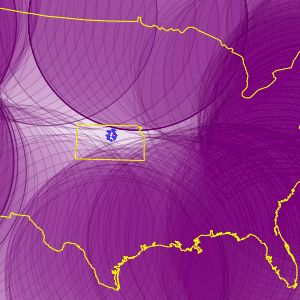
沿等距离的边境绘制300个半径为650英里的地理圆盘. 剩下的未被覆盖的小空白是从边境到美国内部650英里以外区域.

In[6]:=

X GeoGraphics[{GeoStyling[Opacity[0.03], Purple, EdgeForm[ Directive[Thin, Darker[Purple]]]], (GeoDisk[#1, Quantity[650, "Miles"]] &) /@ f[Range[first, last, last/300]], GeoStyling[EdgeForm[Yellow], Opacity[0]], polygon}, GeoRange -> GeoBounds[polygon], GeoBackground -> None, ImageSize -> Large]

Out[6]=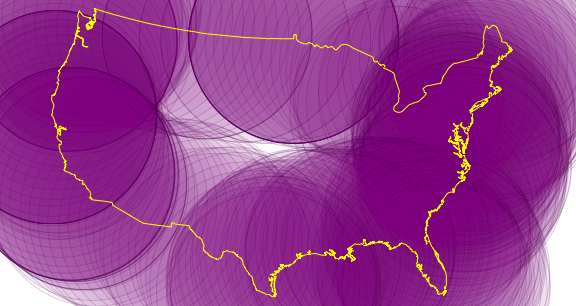

用交互式坐标工具在该区域内选择一点.

In[7]:=

X point = GeoPosition[{39.2, -98.2}];

找出距离该点最近的30个城市.

In[8]:=

X cities = GeoNearest["City", point, 30]

Out[8]=

计算从这些城市到该点的距离.

In[9]:=

X GeoDistance[cities, point]

Out[9]=

计算从这些城市到美国边境最近点的距离. 由于在边境内，距离为负数. 验证 Barnard 确实是距离边境最远的城市.

In[10]:=

X GeoDistance[cities, Polygon@GeoPosition@polygon[[1, 1, 1]], DistanceFunction -> "SignedBoundary"]

Out[10]=

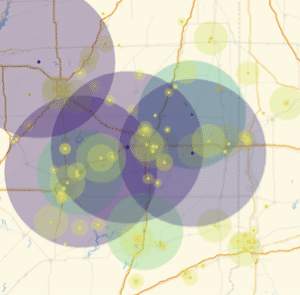
这些城市都在堪萨斯州. 重复地图，并绘制城市和堪萨斯州.

In[11]:=

X GeoGraphics[{GeoStyling[Opacity[0.03], Purple, EdgeForm[ Directive[Thin, Darker[Purple]]]], (GeoDisk[#1, Quantity[650, "Miles"]] &) /@ f[Range[first, last, last/300]], GeoStyling[EdgeForm[Yellow], Opacity[0]], polygon, Polygon[Entity[ "AdministrativeDivision", {"Kansas", "UnitedStates"}]], Blue, PointSize[Small], Point[cities], Red, Point[cities[[1]]]}, GeoRange -> GeoBounds[polygon], GeoBackground -> None, ImageSize -> Large]

Out[11]=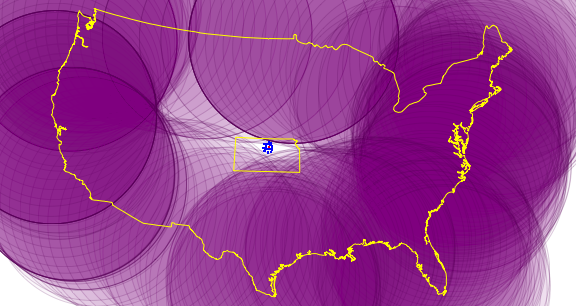