Explore the Earth's Curvature
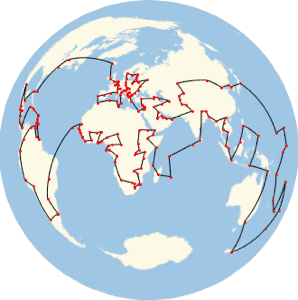
Show how the Earth's curvature affects paths on its surface.
Define a path that starts at the Eiffel Tower and travels 100 km along geodesic lines in each of the four compass directions in turn.
| In[1]:= |  X |
Draw the four path segments and zoom in to verify that they do not close due to the Earth's curvature.
| In[2]:= |  X |
| Out[2]= |  |
Find the distance between the start and finish points.
| In[3]:= | X |
| Out[3]= |
Now follow loxodrome segments (curves of constant rhumb) instead of geodesics.
| In[4]:= |  X |
The latitude of the final point coincides with that of the beginning, but not its longitude.
| In[5]:= |  X |
| Out[5]= | 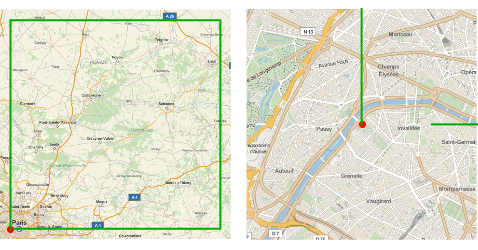 |
Find the distance between the start and finish points.
| In[6]:= | X |
| Out[6]= |