Find the Most Interior Point in the United States
Get a list of {latitude, longitude} coordinates along the border of the United States.
| In[1]:= |  X |
Compute the distances in miles between consecutive points and accumulate them.
| In[2]:= | X |
| In[3]:= | X |
| Out[3]= |  |
This is the total estimated length of the boundary in miles.
| In[4]:= | X |
| Out[4]= |
Construct a parametrization of the boundary.
| In[5]:= | X |
| Out[5]= |  |
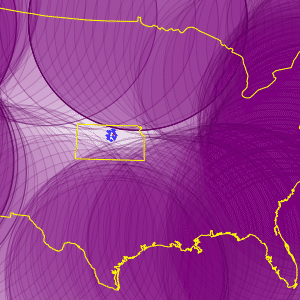
Draw 300 geo disks with 650-mile radius along equidistant points of the boundary. The small space left uncovered is the area of the US farther than 650 miles from the boundary.
| In[6]:= |  X |
| Out[6]= | 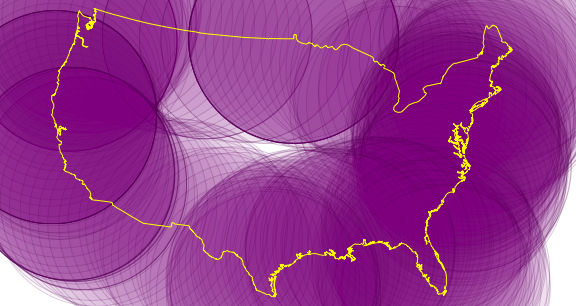 |
Using the interactive coordinate tools, select a point inside that region.
| In[7]:= | X |
Find the 30 nearest cities to that point.
| In[8]:= | X |
| Out[8]= |  |
Compute the distances from those cities to the point.
| In[9]:= | X |
| Out[9]= |  |
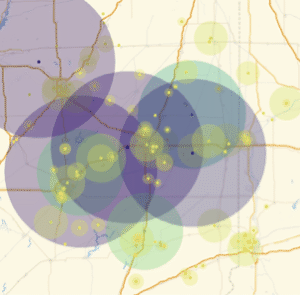
Compute the distance from those cities to the closest point of the US boundary. The distances are negative numbers because we are inside the boundary. Verify that Barnard is in fact the city furthest away from the boundary.
| In[10]:= | X |
| Out[10]= |  |
The cities are all in Kansas. Repeat the map, plotting the cities and the state of Kansas as well.
| In[11]:= |  X |
| Out[11]= | 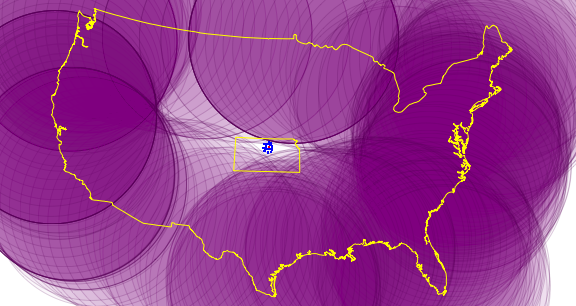 |