Use a Levy Flight to Find Stonehenge in England 

Use so‐called Levy flights, which are optimal for searching, to find Stonehenge within England.

Get the polygon of England and the coordinates of Stonehenge.

In[1]:=

X polygon = Entity["AdministrativeDivision", {"England", "UnitedKingdom"}][ EntityProperty["AdministrativeDivision", "Polygon"]]; stonehenge = Entity["Building", "Stonehenge"][ EntityProperty["Building", "Position"]];

Assuming Stonehenge is visible from a distance of 2 km, define a predicate that tests whether Stonehenge can be seen from a given location.

In[2]:=

X stonehengeVisibleQ[start_, {dist_, dir_}] := With[{m = Floor[dist/1000]}, Min[(GeoDistance[GeoPosition[#1], stonehenge] &) /@ GeoDestination[start, GeoDisplacement[{(Range[0, m] dist)/m, dir}]][[1]]] < Quantity[2, "Kilometers"]]

Starting from the Big Ben, carry out a Levy walk until Stonehenge comes into sight.

In[3]:=

X searchpath = {Entity["Building", "ClockTower"][ EntityProperty["Building", "Position"]]}; mr = DiscretizeGraphics[Polygon[Reverse /@ polygon[[1, 1, -1]]]]; While[ {d, \[Alpha]} = { 1000 RandomVariate[StableDistribution[1, 1, 1, 10, 2]], RandomReal[{0, 360}]}; gd = GeoDestination[Last[searchpath], GeoDisplacement[{d, \[Alpha]}]]; If[sd = SignedRegionDistance[mr, Reverse[First[ gd = GeoDestination[Last[searchpath], GeoDisplacement[{d, \[Alpha]}]] ]]] < 0, ! stonehengeVisibleQ[Last[searchpath], {d, \[Alpha]}], True], If[sd, AppendTo[searchpath, gd]]]

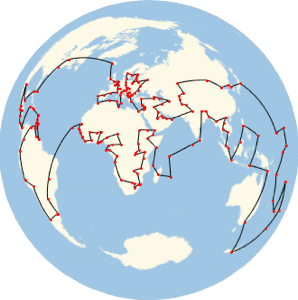
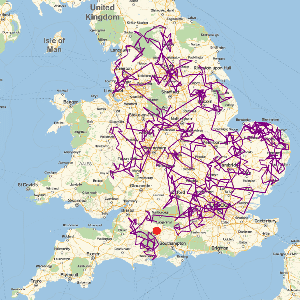
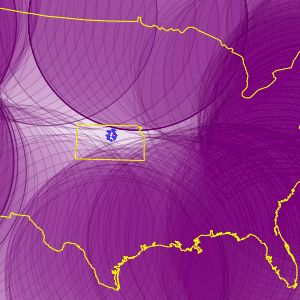
Show the search path.

In[4]:=

X GeoGraphics[{GeoStyling["StreetMap"], polygon , PointSize[Medium], RGBColor[1, 0, 0], Point[stonehenge], RGBColor[ 0.5, 0, 0.5], Thickness[Small], GeoPath[searchpath]}]

Out[4]=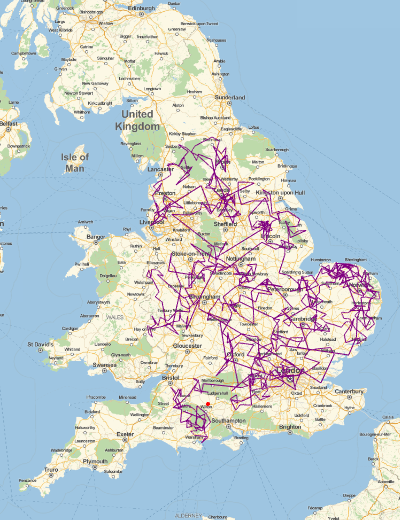