倒立振り子:記号的モデルの線形化
線形化することによって,作用点についての非線形系を調べるために線形系のツールが使えるようになります.この例では倒立振り子を,その直立位置を中心に線形化します.振り子の長さを変化させて,制御された倒立振り子系の挙動を解析します.
モデル
この例では,振り子を直立位置に保つためにPID制御器が使用されています.振り子のピボットポイントは水平方向に移動できるカートに取り付けられており,モーターとギアの配置によって制御されます.
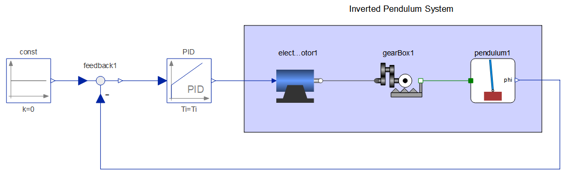
制御系のモデル
制御設計
倒立振り子系は直立位置を中心に線形化されます.振り子の長さは記号形式で保持されます.制御系は,さまざまな長さの振り子の対するPIDパラメータを調整することで設計されます.
SystemModeler 12.0の新機能
選択した記号的パラメータを使って記号的線形化が得られます.
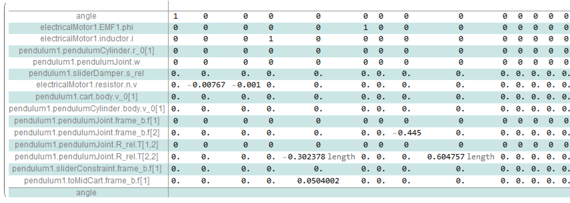
記号パラメータとして線形化された,振り子の長さを含む状態空間表現
PID制御器と倒立振り子からなる複合系は,ナイキスト線図を使用して安定性が検証されます.複合系の開ループ伝達関数には不安定極が1つあり,反時計回りに{-1,0}の周りを一度回転します.不安定極と回転は相殺されるため,閉ループ系には不安定極がないと推測できます.
安定性の検証
ナイキスト線図を使って閉ループ系の不安定極を調べます.
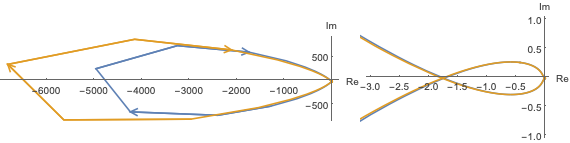
さまざまな長さに対するナイキスト線図
安定性を検証した後,モデルのシミュレーションを実行します.これで振動の生データを観察し,応答のエンベロープをプロットすることができます.長さが増加すると,定常状態に到達するまでの時間が長くなることが分かります.
制御器の配備
さまざまな長さに対する系の挙動を観察します.
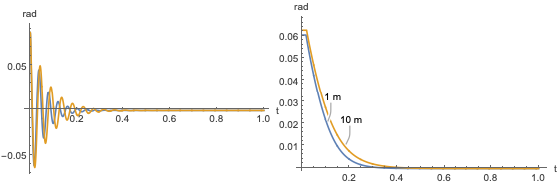
初期の振り子角度5°に対する系の応答
Wolfram System Modeler
評価版
ご購入
System ModelerはWindows,macOS,
Linuxで
日本語と英語でご利用になれます »
ご質問やコメントはWolframエキスパートまでお寄せください »