Mechanical Engineering
Use System Modeler to model and simulate dynamics problems including mechanisms and machinery with kinematic, dynamic, and thermal behaviors. Study and solve vibration problems.
Model Inversion Control of a Hoist Crab
Models can be of great use when designing controllers. In this example, a model of a hoist crab is used to demonstrate the application of model inversion control in controlling nonlinear systems.
To run this example, you'll need
The latest versions of System Modeler and Mathematica.
Please make a selection:
Get afree trial Continue
with download
The System
Hoist crabs are commonly used in bridge cranes to carry the hoist and its potential load across the bridge’s span. When moving the crab, it is important to keep the load from swinging around, as this could potentially cause damage not only to the crane and load, but also to surrounding equipment and material.
The Model and Controller
The crab model includes a horizontally moving crab connected to a load-bearing rope. Model inversion control is used to calculate the force necessary to move the crab and load to a certain specified horizontal position.
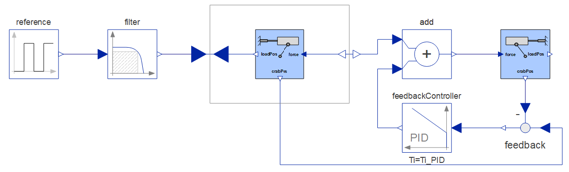
The block Modelica.Blocks.Math.InverseBlockConstraints is used to invert the crab and load model by simply connecting its inputs and outputs. The controller itself consists of a reference signal that specifies the desired load position, a filter, the inverted model, and finally a feedback controller, which in this case is a PID regulator.
Simulation Results
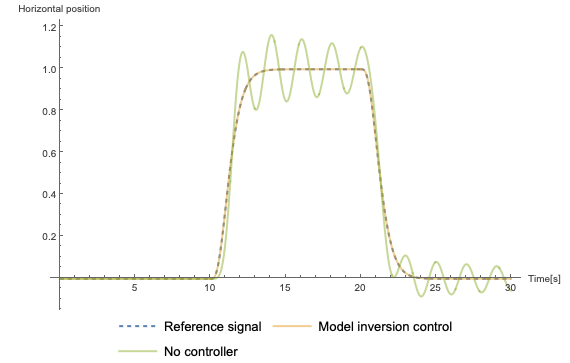
The horizontal position of the load with and without the use of the controller. If we were to move the crab based only on the reference position, the load would start swinging. However, by using the controller, the oscillations can be canceled out and the load can be moved quickly and with precision, closely following the reference signal.
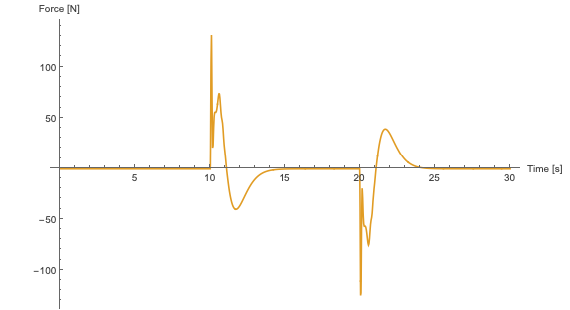
The control signal (input force) used by the controller to move the crab and load to the desired positions. The signal is based on both the inverted model and the feedback controller.
Wolfram System Modeler
Try
Buy
System Modeler is available in English
and Japanese
on Windows, macOS & Linux »
Questions? Comments? Contact a Wolfram expert »