Physics
Expand the curriculum with exciting experiments in dynamics and gain insight into how modeling and simulation can enhance and strengthen understanding of physics and math concepts.
Bend It Like Beckham
Ever wondered how Roberto Carlos or David Beckham could fool goalkeepers by putting a spin on the ball? Maybe not, since they are so good, but have you wondered why the spin actually changes the trajectory of the ball? This example models a free kick in soccer and examines what happens.
To run this example, you'll need
The latest versions of System Modeler and Mathematica.
Please make a selection:
Get afree trial Continue
with download
Watch a free kick with the Magnus force in effect. The forces (Magnus: red, drag: green) and velocity (blue) vectors are shown in the animation of the simulation.
The Model
All that a free kick model needs is essentially a ball that can move and rotate. The tricky part is to assign the correct forces that act on the ball, depending on velocity and spin. Three forces affect the ball: gravity (downward force), drag (force opposing the velocity vector), and the Magnus force (depending on velocity, angular velocity, and spin axis).
Diagram view of the Free Kick model with the Ball component. Magnus and Drag forces, as well as a visualization and contact element, are connected to a body to transform the body into a football.
Magnus Force and Drag Force
The Magnus force is dependent on the spin and velocity. All other variables contributing to the Magnus force can be put into a so-called "lift coefficient", Cl. This lift coefficient is difficult to calculate analytically and is often measured from experiments. The left plot below shows experimental data of the lift coefficient to spin ratio (=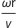 
, rotational velocity times radius divided by velocity) and the function that is used to approximate Cl. The drag force is dependent on the velocity and the Reynolds number. The right plot shows experimental data of the drag coefficient compared to the Reynolds number, with the approximated function for Cd used in the model.
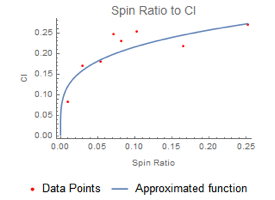
Lift coefficient for different spin ratios.
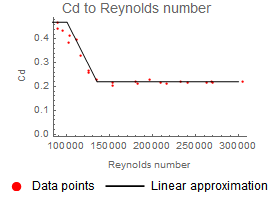
Drag coefficient for different Reynolds number.
What initial velocity and spin are required to score a goal directly from a corner kick?
The forces (Magnus: red, drag: green) and velocity (blue) vectors are shown in the animation of the simulation.
Visualize the forces automatically
Depending on velocity and spin, the forces are calculated, and the velocity vector will be continuously changing due to the forces acting on the ball.
The initial velocity and spin required to score can be calculated analytically, or alternatively (the more convenient way), be tested by making simulations and analyzing the resulting animation to see which initial parameter needs to be tuned. One example of initial conditions to score from the corner position is initVel = {35, 8, 12} m/s and initAngVel = {0, 50, 10} rad/s. See the video for a nice corner goal!
300 Corner Kicks at Once
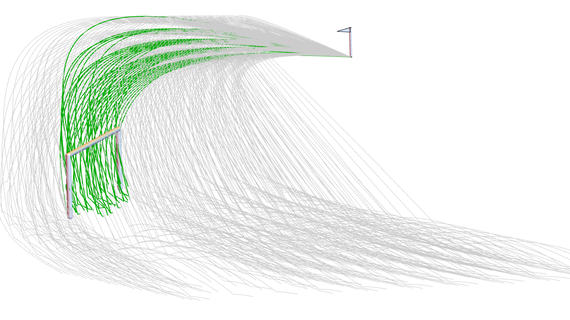
Trajectories of 300 corner kicks with different initial velocities for every kick. Gray trajectories are misses and green trajectories are goals.
If you find that simulating one kick at a time is too slow, Mathematica can help you out using WSMLink and parameter sweep. In the graphic above, 300 simulations with different initial velocities were done at the same time. Out of the 300 hundred trajectories, 45 scored and 255 missed. Imagine if Beckham had access to SystemModeler and Mathematica in his glory days, how he could have optimized his free kicks!
Wolfram System Modeler
Try
Buy
System Modeler is available in English
and Japanese
on Windows, macOS & Linux »
Questions? Comments? Contact a Wolfram expert »