ベッカムのようにボールの軌道を曲げる
ロベルト・カルロスやデビッド・ベッカムがボールに回転をかけてゴールキーパーを騙すことができるのはなぜか考えたことがありますか． 彼らのプレーは素晴らしいので不思議に思わないかもしれませんが，回転によってボールの軌道が実際に変わるのはなぜか考えたことはありますか．この例ではサッカーのフリーキックをモデル化し，何が起こっているのかを調べます．
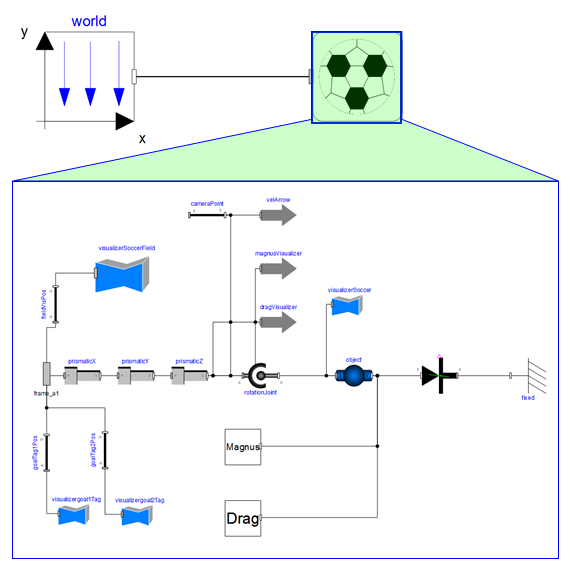
マグナス力が作用するフリーキックを見てみる．力（マグナス力：赤，抗力：緑）と速度（青）のベクトルがシミュレーションのアニメーションに表示される
モデル
フリーキックモデルに必要なのは，基本的に移動および回転できるボールだけです．難しいのは，速度とスピンに応じてボールに作用する正しい力を割り当てることです．ボールには重力（下向きの力），抗力（速度ベクトルに反対する力），マグナス力（速度，角速度，スピン軸に応じて異なる）の 3 つの力が影響します．
ボールコンポーネントを含むフリーキックモデルのダイアグラムビュー．マグナス力と抗力，および視覚化要素と接触要素がボディーに接続され，ボディーがサッカーボールに変換される．
マグナス力と抗力
マグナス力はスピンと速度に依存します．マグナス力に寄与する他のすべての変数は，いわゆる「揚力係数」，Cl にまとめることができます．この揚力係数は解析的に計算するのが難しく，多くの場合は実験から測定されます．左下のグラフは，揚力係数とスピンの比率（=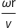 
，回転速度×半径÷速度）の実験データと，Cl を近似するために使用される関数を示しています．抗力は速度とレイノルズ数に依存します．右側のグラフは，モデルで使用される Cd の近似関数を使用して，レイノルズ数と比較した抗力係数の実験データを示しています．
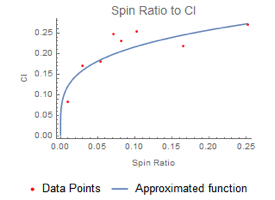
さまざまなスピン率に対する揚力係数
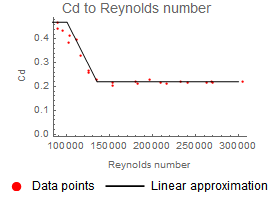
さまざまなレイノルズ数に対する抗力係数
コーナーキックから直接ゴールを決めるには，どの程度の初速度とスピンが必要でしょうか．
シミュレーションのアニメーションには，力（マグナス力：赤，抗力：緑）と速度（青）のベクトルが表示される．
力を自動的に可視化する
速度とスピンに応じて力が計算され，ボールに作用する力のために速度ベクトルが継続的に変化します．
得点に必要な初期速度とスピン量は，解析的に計算することも，（より便利な方法として）シミュレーションを行って結果のアニメーションを分析し，どの初期パラメータを調整する必要があるかを調べてテストすることもできます．コーナー位置から得点するための初期条件の一つの例は，initVel = {35, 8, 12} m/sおよびinitAngVel = {0, 50, 10} rad/sです．動画で素晴らしいコーナーゴールをご覧ください．
一度に300回のコーナーキック
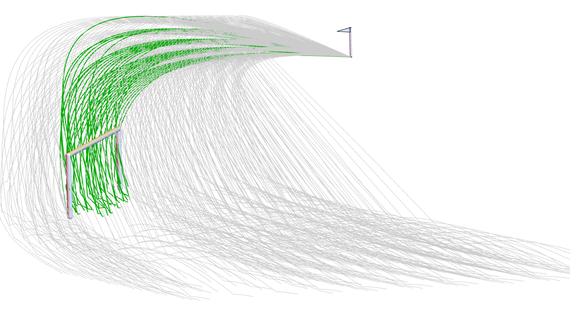
キックごとに異なる初期速度で行われた300回のコーナーキックの軌道．灰色の軌道は失敗，緑色の軌道はゴールである．
キックを1回ずつシミュレーションするのは遅すぎると感じたら，WSMLink とパラメータスイープを使ったMathematicaが役立ちます．上のグラフィックスでは，異なる初期速度で300回のシミュレーションが同時に実行されています．300の軌道のうち，45回は成功し255回は失敗しました．ベッカムが全盛期にSystem ModelerとMathematicaにアクセスできていたなら，フリーキックをどれだけ最適化できたか想像してみてください．
Wolfram System Modeler
評価版
ご購入
System ModelerはWindows，macOS，
Linuxで
日本語と英語でご利用になれます »
ご質問やコメントはWolframエキスパートまでお寄せください »