Wolfram言語™

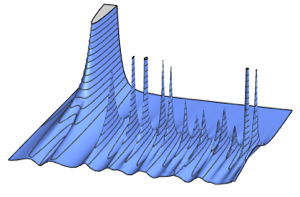
行列のスペクトル密度

多くの行列分布のスペクトル密度は，対応する普遍的な極限形を持つ．独立項を含むハミルトニアンランダム行列にとって，これはウィグナーの半円則である．

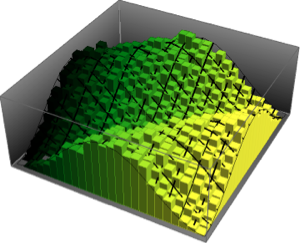
ガウス型アンサンブルについては，行列のスケールされたスペクトル密度は，量子調和振動子の固有関数と関係する有限行列次元について閉形式を持つ．

スケールされたガウス型ユニタリアンサンブルのスペクトルを表し，その結合スペクトル密度の閉形式の式を提供するためには，MatrixPropertyDistributionを使用する．

In[1]:=

scaledSpectrum\[ScriptCapitalD][n_] := MatrixPropertyDistribution[ Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed] GaussianUnitaryMatrixDistribution[n]];

In[2]:=

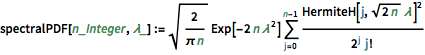
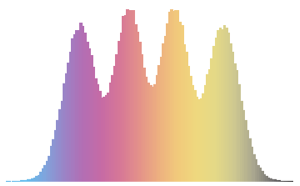
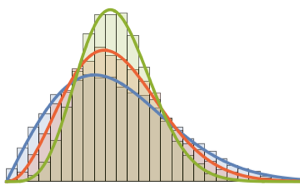
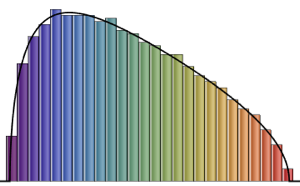
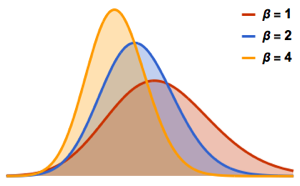
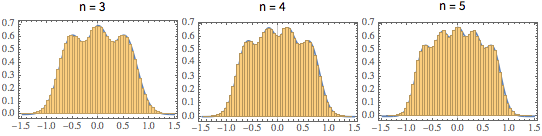
spectralPDF[n_Integer, \[Lambda]_] := Sqrt[2/(\[Pi] n)] Exp[-2 n \[Lambda]^2] \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(n - 1\)] \*FractionBox[ SuperscriptBox[\(HermiteH[j, \*SqrtBox[\(2\ n\)]\ \[Lambda]]\), \(2\)], \( \*SuperscriptBox[\(2\), \(j\)]\ \(j!\)\)]\)

密度極大値の数が行列サイズに等しく次元が低い行列には，特徴的な振動パターンが見られる．

In[3]:=

scaledSpectra = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#], 10^5]] & /@ {3, 4, 5};

In[4]:=

Row@MapThread[ Show[Plot[spectralPDF[#1, x], {x, -1.5, 1.5}, PlotTheme -> "Scientific", PlotStyle -> ColorData[97, 1], PlotLegends -> Placed["n = " <> ToString@#1, Above]], Histogram[#2, {0.05}, PDF]] &, {{3, 4, 5}, scaledSpectra}]

Out[4]=

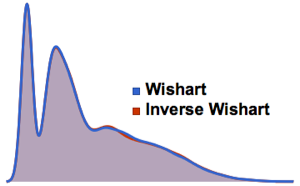
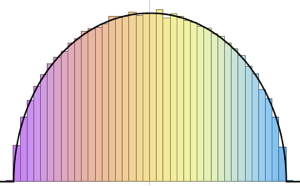
次元が高い極限では，密度がWignerSemicircleDistributionに収束する．

In[5]:=

n = 250; scaledSpectrum = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];

In[6]:=

Show[Histogram[scaledSpectrum, {0.05}, PDF, PlotTheme -> "Detailed"], Plot[PDF[WignerSemicircleDistribution[1], x], {x, -1.5, 1.5}, Exclusions -> None, PlotTheme -> "Scientific", PlotLegends -> None, PlotStyle -> ColorData[97, 1]], ImageSize -> Medium]

Out[6]=