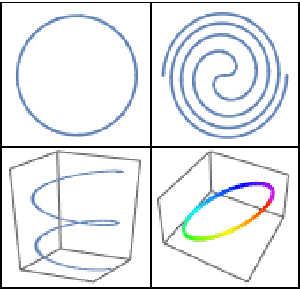
Compute Symbolic Solutions for ODEs with Events 

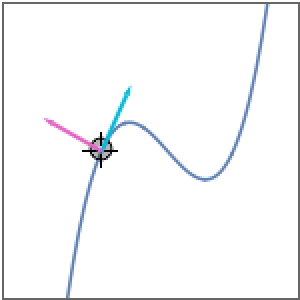
Solve an ODE with a state-dependent event using DSolve.

In[1]:=

X sol = DSolve[{y''[t] == -981/100, y[0] == 5, y'[0] == 0, WhenEvent[y[t] == 0, y'[t] -> -(7/10) y'[t]]}, y[t], {t, 0, 5}]

Out[1]=

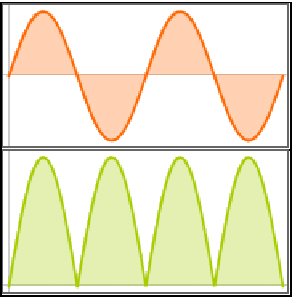
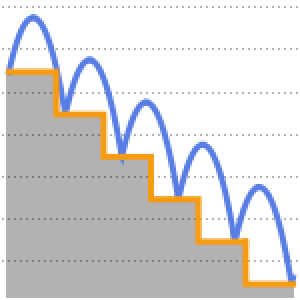
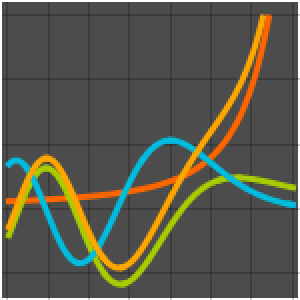
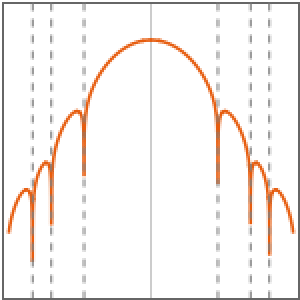
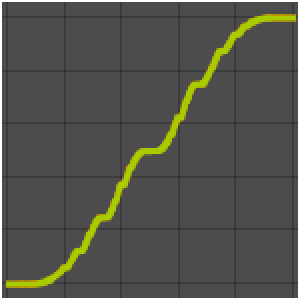
This system models a bouncing ball.

In[2]:=

X Plot[y[t] /. sol, {t, 0, 5}, Filling -> Axis]

Out[2]=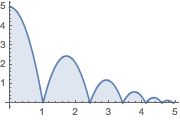

Stop the integration of an ODE when an event occurs.

In[3]:=

X DSolve[{x'[t] == -x[t], x[0] == 1, WhenEvent[t == 3, "StopIntegration"]}, x, {t, 0, 4}]

Out[3]=

Remove an event after it has occurred once.

In[4]:=

X sol = DSolve[{x''[t] + x[t] == 0, x[0] == 0, x'[0] == 1, WhenEvent[x[t] == 0, {x'[t] -> -x'[t], "RemoveEvent"}]}, x, {t, 0, 10}]

Out[4]=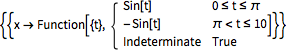

In[5]:=

X Plot[x[t] /. sol, {t, 0, 10}]

Out[5]=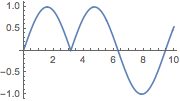

Specify that a variable maintains its value between events.

In[6]:=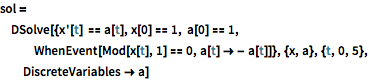

X sol = DSolve[{x'[t] == a[t], x[0] == 1, a[0] == 1, WhenEvent[Mod[x[t], 1] == 0, a[t] -> - a[t]]}, {x, a}, {t, 0, 5}, DiscreteVariables -> a]

Out[6]=

In[7]:=

X Plot[Evaluate[{x[t], a[t]} /. sol], {t, 0, 4}, Exclusions -> None]

Out[7]=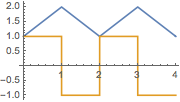