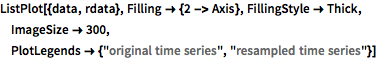Work with Irregular Time Series
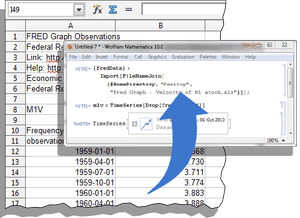
Draw a sample of Poisson process, sampled at the random times of arrivals.
| Out[1]= | 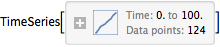 |
| Out[2]= |  |
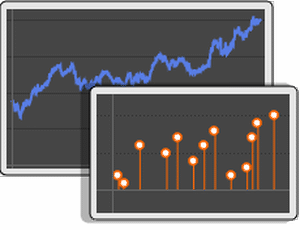
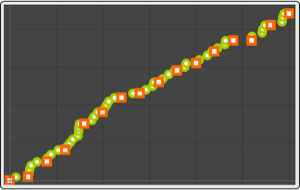
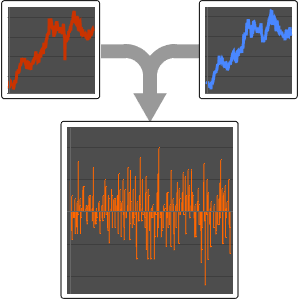
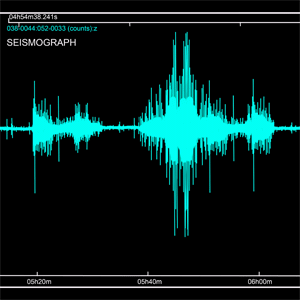
Visualize the time series.
| Out[3]= | 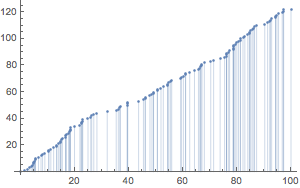 |
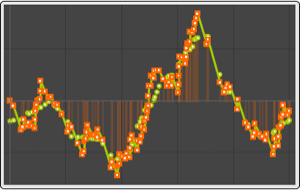
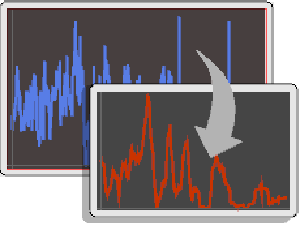
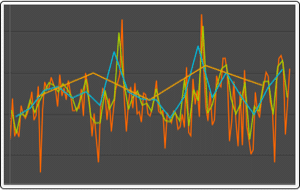
Use TimeSeriesMapThread to subtract the mean function from the time series.
| Out[5]= | 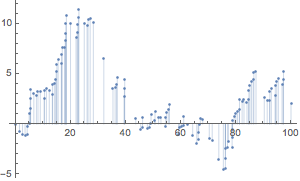 |
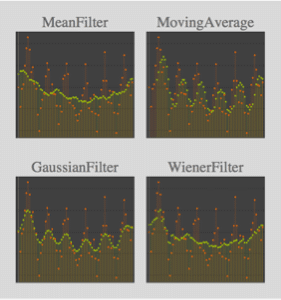
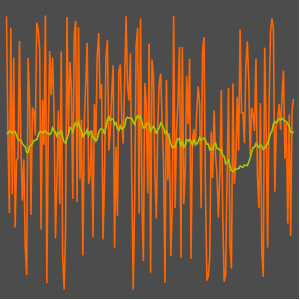
Use MovingMap to compute mean over a centered constant‐width sliding window.
show complete Wolfram Language inputhide input
| Out[7]= | 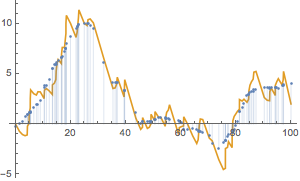 |
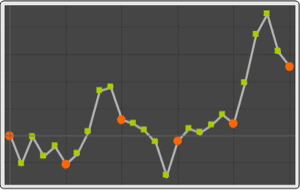
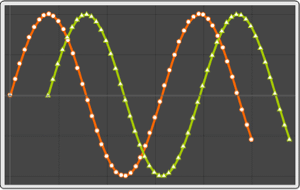
Use TimeSeriesAggregate to build regularly spaced time series of the largest values in non-overlapping windows of constant width.
show complete Wolfram Language inputhide input
| Out[9]= | 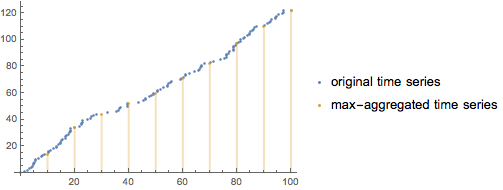 |
| Out[10]= |  |
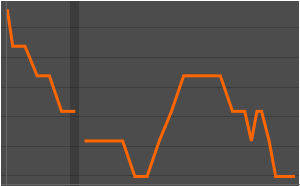
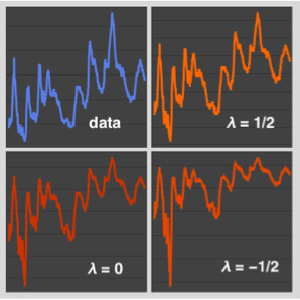
Resample with a step of 10 using interpolation of order 0.
show complete Wolfram Language inputhide input
| Out[12]= | 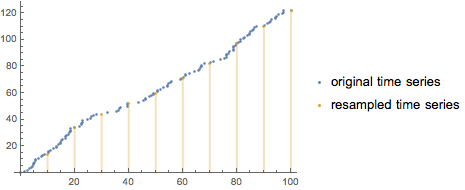 |
| Out[13]= |  |
Treat the original time series as regularly sampled for use in functions that require such uniformly sampled input.
| Out[14]= | 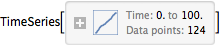 |
| Out[15]= |  |
| Out[16]= |  |