New in Mathematica 9
Time Series and Stochastic Differential Equations
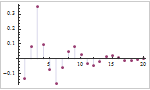
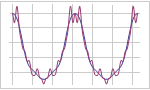
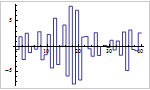
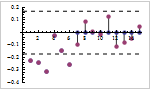
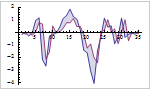
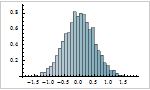
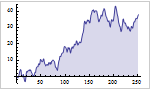
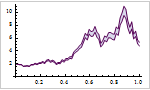
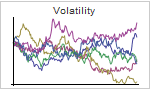
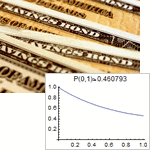
Mathematica 9 adds extensive support for time series and stochastic differential equation (SDE) random processes. A full suite of scalar and vector time series models, both stationary or supporting polynomial and seasonal components, is included. Time series models can easily be simulated, estimated from data, and used to generate forecasts. Both parametric and fully general Ito or Stratonovich processes can be used to specify SDE processes. SDE processes can easily be simulated numerically and a number of properties can also be computed symbolically.
- Support for scalar and vector moving average (MA), autoregressive (AR), and ARMA processes.
- Support for processes with polynomial and seasonal trends, as well as long memory time series models.
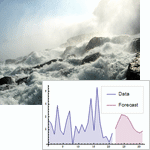
- Full support for simulation, estimation, and forecasting from time series models.
- Additional time series support for partial correlation function and spectral density.
- Flexible tests for unit root including augmented Dickey-Fuller and Phillips-Perron tests.
- Support for parametric stochastic differential equations (SDEs) such as Cox-Ingersoll-Ross.
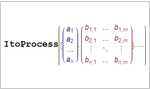
- Support for scalar and vector Ito and Stratonovich processes defined by differential equations.
- Automatic conversion of parametric SDE processes to their Ito and Stratonovich forms.
- Support for Ito and Stratonovich SDE processes driven by other SDE processes.
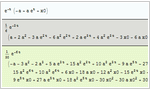
- Support for nonlinear functions of Ito and Stratonovich process with automatic conversion to normal form.
- Extensive methods for simulation of SDE processes including Euler-Maruyama, stochastic Runge-Kutta, etc.
- Support for symbolically computing mean function, covariance function for time series, and SDE processes.
RELATED FUNCTIONSRandomFunction 
ARMAProcess ARIMAProcess SARIMAProcess ARProcess MAProcess PowerSpectralDensity WeakStationarity ProcessParameterAssumptions TimeSeriesInvertibility TemporalData EstimatedProcess PartialCorrelationFunction KalmanFilter UnitRootTest SARMAProcess ProcessEstimator CorrelationFunction TimeSeriesForecast FindProcessParameters FARIMAProcess ItoProcess WienerProcess GeometricBrownianMotionProcess OrnsteinUhlenbeckProcess CoxIngersollRossProcess BrownianBridgeProcess StratonovichProcess SliceDistribution StationaryDistribution CovarianceFunction AbsoluteCorrelationFunction AdjustTimeSeriesForecast
ARMAProcess ARIMAProcess SARIMAProcess ARProcess MAProcess PowerSpectralDensity WeakStationarity ProcessParameterAssumptions TimeSeriesInvertibility TemporalData EstimatedProcess PartialCorrelationFunction KalmanFilter UnitRootTest SARMAProcess ProcessEstimator CorrelationFunction TimeSeriesForecast FindProcessParameters FARIMAProcess ItoProcess WienerProcess GeometricBrownianMotionProcess OrnsteinUhlenbeckProcess CoxIngersollRossProcess BrownianBridgeProcess StratonovichProcess SliceDistribution StationaryDistribution CovarianceFunction AbsoluteCorrelationFunction AdjustTimeSeriesForecast
