複素数の表現

新関数のReImとAbsArgでは，複素数をその直交表現あるいは極表現に簡単に変換することができる．

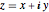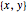複素数 を順序対に変換する．

In[1]:=

ReIm[3 + 4 I]

Out[1]=

いくつかの数を変換する．

In[2]:=

ReIm[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[2]=

複素数 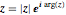を順序対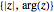に変換する．

In[3]:=

AbsArg[3 + 4 I]

Out[3]=

いくつかの数を変換する．

In[4]:=

AbsArg[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[4]=

複素数値の関数を，複素平面上の曲線としてプロットする．

In[5]:=

ParametricPlot[ReIm[(-2)^x], {x, 0, 4}]

Out[5]=

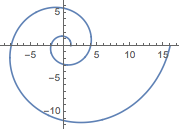
複素平面プロットの中の特定の点に注釈を付ける．

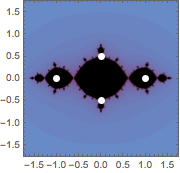
In[6]:=

JuliaSetPlot[-1, PlotRange -> 1.75, Epilog -> {PointSize[Large], White, Point[ReIm[{I/2, -I/2, 1, -1}]]}]

Out[6]=