Representações de números complexos

As novas funções ReIm e AbsArg facilitam a conversão de números complexos para sua representação cartesiana ou polar.

Converta o número complexo 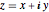para um par ordenado .

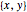In[1]:=

ReIm[3 + 4 I]

Out[1]=

Converta vários números.

In[2]:=

ReIm[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[2]=

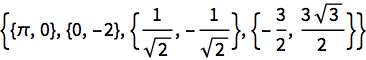
Converta o número complexo 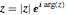para um par ordenado .

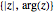In[3]:=

AbsArg[3 + 4 I]

Out[3]=

Converta vários números.

In[4]:=

AbsArg[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[4]=

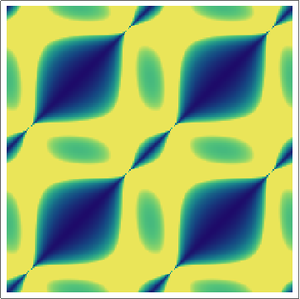
Faça um gráfico de uma função complexa como uma curva no plano complexo.

In[5]:=

ParametricPlot[ReIm[(-2)^x], {x, 0, 4}]

Out[5]=

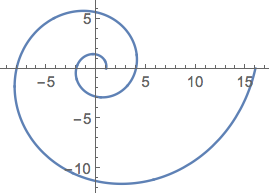
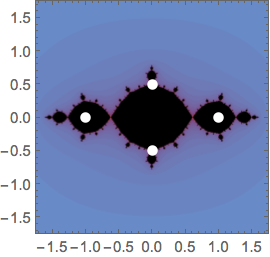
Anote os pontos complexos em um gráfico de planos complexos.

In[6]:=

JuliaSetPlot[-1, PlotRange -> 1.75, Epilog -> {PointSize[Large], White, Point[ReIm[{I/2, -I/2, 1, -1}]]}]

Out[6]=