复数表示

新函数 ReIm 和 AbsArg 使得将一个复数转换为笛卡儿坐标或极坐标表示变得很容易.

将复数 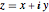转换为有序数据对 .

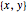In[1]:=

ReIm[3 + 4 I]

Out[1]=

转换更多数字.

In[2]:=

ReIm[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[2]=

将复数 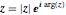转换为有序数据对 .

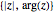In[3]:=

AbsArg[3 + 4 I]

Out[3]=

转换更多数字.

In[4]:=

AbsArg[{Pi, -2 I, Sqrt[-I], 3 Exp[I 2 Pi/3]}]

Out[4]=

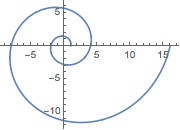
在复平面上绘制复值函数的曲线.

In[5]:=

ParametricPlot[ReIm[(-2)^x], {x, 0, 4}]

Out[5]=

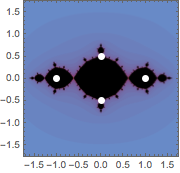
复平面图中标注特定点.

In[6]:=

JuliaSetPlot[-1, PlotRange -> 1.75, Epilog -> {PointSize[Large], White, Point[ReIm[{I/2, -I/2, 1, -1}]]}]

Out[6]=