Solve Combinatorial Problems Using Permanent
A permanent is similar to a determinant, except that all terms have a positive sign.
In[1]:=
Permanent[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
SubscriptBox["a",
RowBox[{"1", ",", "1"}]],
SubscriptBox["a",
RowBox[{"1", ",", "2"}]]},
{
SubscriptBox["a",
RowBox[{"2", ",", "1"}]],
SubscriptBox["a",
RowBox[{"2", ",", "2"}]]}
},
GridBoxAlignment->{
"Columns" -> {{Left}}, "ColumnsIndexed" -> {},
"Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]Out[1]=
In[2]:=
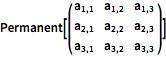
Permanent[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
SubscriptBox["a",
RowBox[{"1", ",", "1"}]],
SubscriptBox["a",
RowBox[{"1", ",", "2"}]],
SubscriptBox["a",
RowBox[{"1", ",", "3"}]]},
{
SubscriptBox["a",
RowBox[{"2", ",", "1"}]],
SubscriptBox["a",
RowBox[{"2", ",", "2"}]],
SubscriptBox["a",
RowBox[{"2", ",", "3"}]]},
{
SubscriptBox["a",
RowBox[{"3", ",", "1"}]],
SubscriptBox["a",
RowBox[{"3", ",", "2"}]],
SubscriptBox["a",
RowBox[{"3", ",", "3"}]]}
},
GridBoxAlignment->{
"Columns" -> {{Left}}, "ColumnsIndexed" -> {},
"Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]Out[2]=
Thus, applying Permanent to a matrix whose entries all equal 1 is a fun but inefficient way to compute the factorial function.
In[3]:=
Table[Permanent[ConstantArray[1, {n, n}]], {n, 10}]Out[3]=
The permanent can be used to solve the following more interesting combinatorial problem: given  sets, each containing a subset of
sets, each containing a subset of 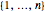 , how many ways are there to choose a distinct element from each subset? First, construct the matrix
, how many ways are there to choose a distinct element from each subset? First, construct the matrix 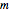 where the
where the 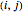 position contains a 1 when subset
position contains a 1 when subset  contains
contains 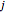 , and zero otherwise.
, and zero otherwise.
In[4]:=
sets = {{3, 5, 6, 7}, {3, 7}, {1, 2, 4, 5, 7}, {3}, {1, 3, 6}, {1, 5,
7}, {1, 2, 3, 6}}Out[4]=
In[5]:=
m = Table[If[MemberQ[sets[[i]], j], 1, 0] , {i, 7}, {j, 7}];
m // MatrixFormOut[5]//MatrixForm=

The permanent of 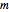 is the solution of the problem.
is the solution of the problem.
In[6]:=
Permanent[m]Out[6]=
Confirm the answer by explicitly constructing all tuples.
In[7]:=
Select[Tuples[sets], DuplicateFreeQ]Out[7]=