Region Moments
Support of polynomial moments of a region in Version 11 provides powerful and flexible tools to compare, classify, and compute properties over regions.
Symbolically calculate moments of regions.
In[1]:=
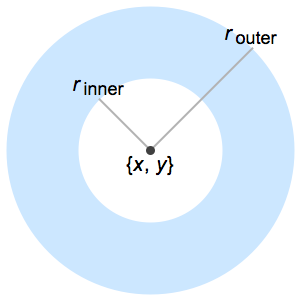
RegionMoment[Disk[], {0, 0}]Out[1]=
In[2]:=
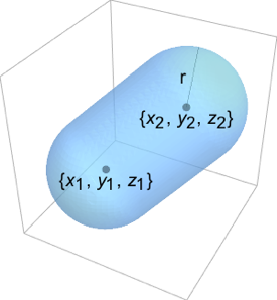
RegionMoment[CapsuleShape[], {2, 0, 0}]Out[2]=
In[3]:=
RegionMoment[Cone[{{0, 0, 0}, {0, 0, 1}}, r], {2, 0, 0}]Out[3]=
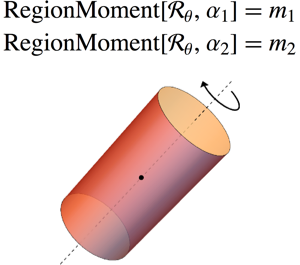
Suppose a region with unknown parameters is provided, along with the knowledge that all zero-order and first-order moments are 1. Find the numerical values of each parameter.
Define the region and the assumptions on its parameters.
In[4]:=
$Assumptions = r > 0 && x > 0 && y > 0 && z > 0;In[5]:=
cyl = Cylinder[{{0, 0, 0}, {x, y, z}}, r];Calculate its zero-order and first-order moments.
In[6]:=
cfs = {{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}};In[7]:=
{m0, m100, m010, m001} = Table[RegionMoment[cyl, c], {c, cfs}]Out[7]=
Solve for the parameters, given that all zero-order and first-order moments are 1.
In[8]:=
sol = Solve[{m0 == 1, m100 == 1, m010 == 1, m001 == 1, $Assumptions}]Out[8]=
Obtain the region.
In[9]:=
cyl /. solOut[9]=
Approximate its radius.
In[10]:=
N[cyl /. sol]Out[10]=