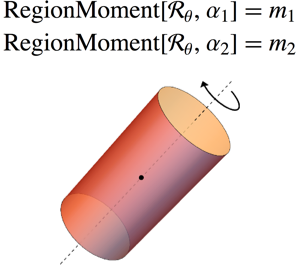
区域矩
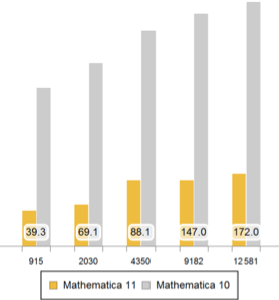
版本 11 对区域的多项式矩的支持为区域的比较、分类及性质计算提供了强大而灵活的工具.
符号式计算区域矩.
In[1]:=
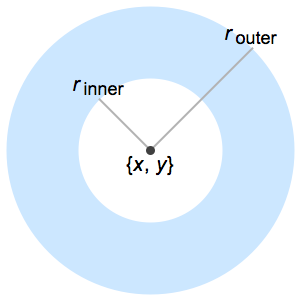
RegionMoment[Disk[], {0, 0}]Out[1]=
In[2]:=
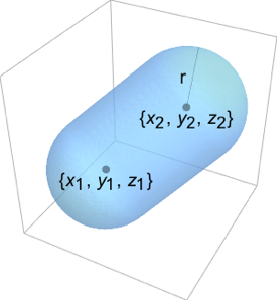
RegionMoment[CapsuleShape[], {2, 0, 0}]Out[2]=
In[3]:=
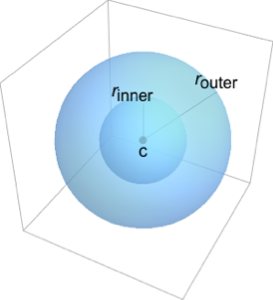
RegionMoment[Cone[{{0, 0, 0}, {0, 0, 1}}, r], {2, 0, 0}]Out[3]=
假设有一个参数未知,但知道所有零阶矩和一阶矩都为 1 的区域,求每个参数的数值.
定义区域以及对其参数的假设.
In[4]:=
$Assumptions = r > 0 && x > 0 && y > 0 && z > 0;In[5]:=
cyl = Cylinder[{{0, 0, 0}, {x, y, z}}, r];计算其零阶矩和一阶矩.
In[6]:=
cfs = {{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 0, 1}};In[7]:=
{m0, m100, m010, m001} = Table[RegionMoment[cyl, c], {c, cfs}]Out[7]=
如果所有零阶矩和一阶矩是 1,求解参数.
In[8]:=
sol = Solve[{m0 == 1, m100 == 1, m010 == 1, m001 == 1, $Assumptions}]Out[8]=
得到区域.
In[9]:=
cyl /. solOut[9]=
半径的近似值.
In[10]:=
N[cyl /. sol]Out[10]=