Substitutionssysteme: Neu in Wolfram Language 11

Substitutionssysteme

SubstitutionSystem generiert eine Liste, die die Evolution eines bestimmten Anfangszustands nach der iterativen Anwendung einiger Regeln darstellt.

Wir gehen vom folgenden Anfangszustand und den folgenden Regeln aus.

In[1]:=

init = "\[Wolf]";
rules = {"\[HappySmiley]" -> "\[Wolf]\[HappySmiley]", 
   "\[Wolf]" -> "\[HappySmiley]"};

Mit SubstitutionSystem können wir die Evolution des Zustands über 8 Iterationen verfolgen.

In[2]:=

SubstitutionSystem[{"\[HappySmiley]" -> "\[Wolf]\[HappySmiley]", 
   "\[Wolf]" -> "\[HappySmiley]"}, "\[Wolf]", 8] // Column

Out[2]=

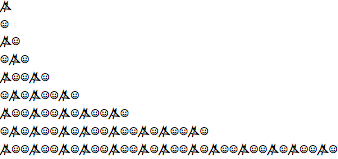
Verwenden Sie eine zweidimensionale Reihe von Regeln, um den Sierpiński-Teppich zu erstellen.

In[3]:=

rules2D = {1 -> {{1, 1, 1}, {1, 0, 1}, {1, 1, 1}}, 
   0 -> ConstantArray[0, {3, 3}]};

Visualisieren Sie dieses Substitutionssystem mittels RulePlot.

In[4]:=

RulePlot@SubstitutionSystem[rules2D]

Out[4]=

Generieren Sie den Sierpiński-Teppich.

In[5]:=

ArrayPlot /@ SubstitutionSystem[rules2D, {{1}}, 5]

Out[5]=