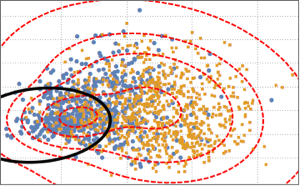
確率変数の積と商の確率密度関数
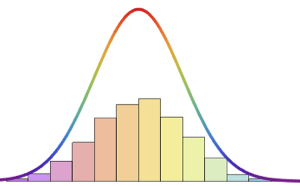
BetaDistribution[2, 3]から独立して  回抽出した場合の最小サンプルに対する最大サンプルの比について確率密度関数を求める.
回抽出した場合の最小サンプルに対する最大サンプルの比について確率密度関数を求める.
In[1]:=

n = 5;
pdf = PDF[
TransformedDistribution[
min/max, {min, max} \[Distributed]
OrderDistribution[{BetaDistribution[2, 3], n}, {1, n}]], u]Out[1]=

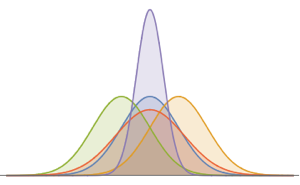
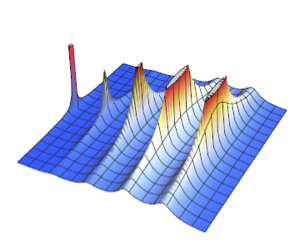
密度を可視化する.
In[2]:=
Plot[pdf, {u, 0, 1}, PlotRange -> All, Filling -> Axis,
PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]Out[2]=
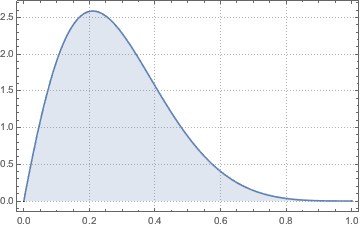
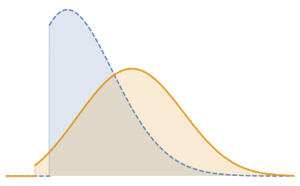
2つの三角分布の積について確率密度関数を計算する.
In[3]:=

pdf2 = PDF[
TransformedDistribution[
x1 x2, {x1 \[Distributed] TriangularDistribution[{-1, 2}, -1],
x2 \[Distributed] TriangularDistribution[{-4, 3}, 2]}], u]Out[3]=
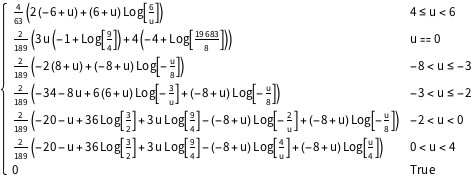
完全なWolfram言語入力を表示する
Out[4]=
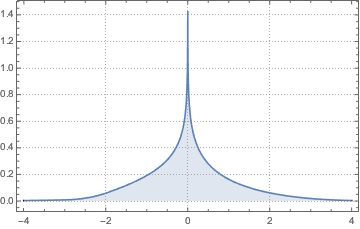
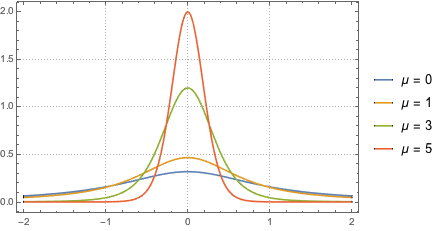
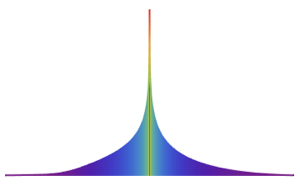
2つの独立した正規確率変数の商について確率密度関数を求める.
In[5]:=

pdf3 = PDF[
TransformedDistribution[
z1/z2, {z1 \[Distributed] NormalDistribution[],
z2 \[Distributed] NormalDistribution[\[Mu], 1]}], x]Out[5]=
分布の裾は,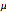 の任意の固定値について重い.
の任意の固定値について重い.
In[6]:=
Series[Exp[\[Mu]^2/2] pdf3, {x, Infinity, 8},
Assumptions -> \[Mu] > 0] // ExpandOut[6]=
完全なWolfram言語入力を表示する
Out[7]=