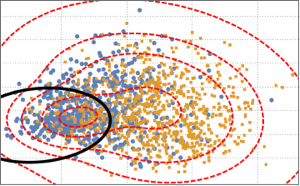
Функция распределения вероятностей для вычислительных операций со случайными величинами
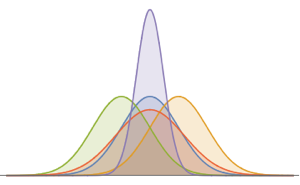
Рассчитаем функцию плотности вероятности (PDF) для соотношения самого маленького и самого большого образца среди n независимых рисунков с помощью функции бета-распределение, BetaDistribution[2, 3].
In[1]:=

n = 5;
pdf = PDF[
TransformedDistribution[
min/max, {min, max} \[Distributed]
OrderDistribution[{BetaDistribution[2, 3], n}, {1, n}]], u]Out[1]=

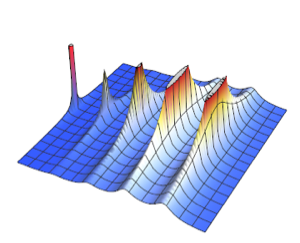
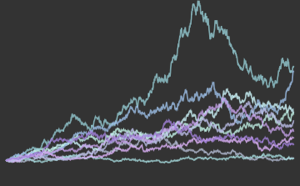
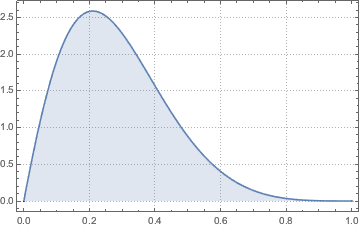
Визуализируем плотность вероятности.
In[2]:=
Plot[pdf, {u, 0, 1}, PlotRange -> All, Filling -> Axis,
PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]Out[2]=
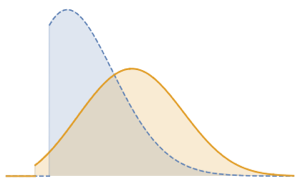
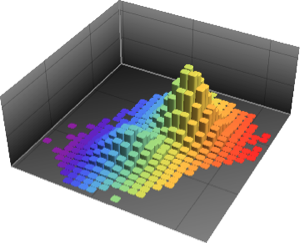
Рассчитаем функцию распределения вероятностей для произведения двух треугольных распределений.
In[3]:=

pdf2 = PDF[
TransformedDistribution[
x1 x2, {x1 \[Distributed] TriangularDistribution[{-1, 2}, -1],
x2 \[Distributed] TriangularDistribution[{-4, 3}, 2]}], u]Out[3]=
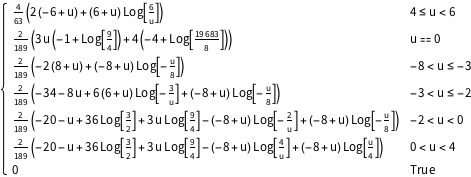
код на языке Wolfram Language целиком
Out[4]=
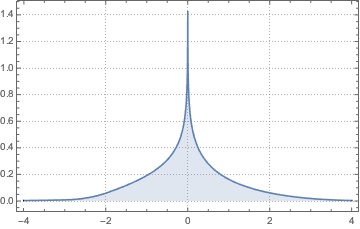
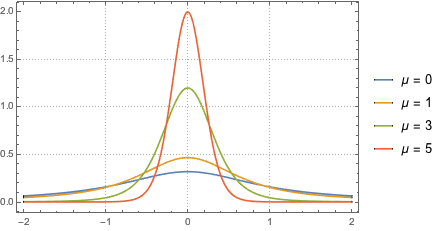
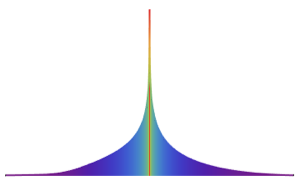
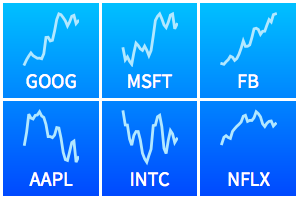
Рассчитатаем функцию распределения вероятностей для отношения двух независимых нормальных случайных величин.
In[5]:=

pdf3 = PDF[
TransformedDistribution[
z1/z2, {z1 \[Distributed] NormalDistribution[],
z2 \[Distributed] NormalDistribution[\[Mu], 1]}], x]Out[5]=
Распределение имеет длинный хвост при любом фиксированном значении 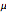 .
.
In[6]:=
Series[Exp[\[Mu]^2/2] pdf3, {x, Infinity, 8},
Assumptions -> \[Mu] > 0] // ExpandOut[6]=
код на языке Wolfram Language целиком
Out[7]=