PDF for Product/Quotients of Random Variables
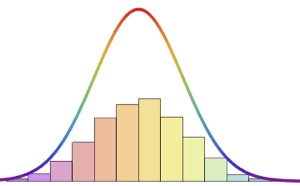
Find the probability density function for the ratio of the smallest to the largest sample among  independent drawings from BetaDistribution[2, 3].
independent drawings from BetaDistribution[2, 3].
In[1]:=

n = 5;
pdf = PDF[
TransformedDistribution[
min/max, {min, max} \[Distributed]
OrderDistribution[{BetaDistribution[2, 3], n}, {1, n}]], u]Out[1]=
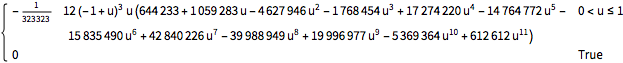
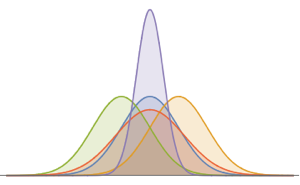
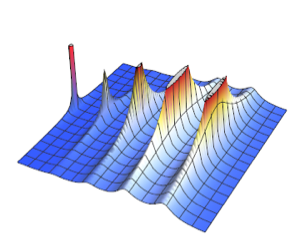
Visualize the density.
In[2]:=
Plot[pdf, {u, 0, 1}, PlotRange -> All, Filling -> Axis,
PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]Out[2]=
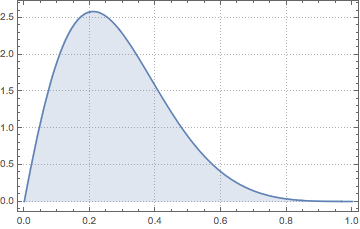
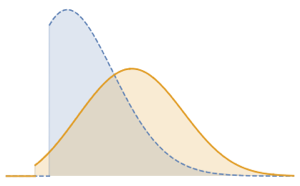
Compute the PDF for the product of two triangular distributions.
In[3]:=

pdf2 = PDF[
TransformedDistribution[
x1 x2, {x1 \[Distributed] TriangularDistribution[{-1, 2}, -1],
x2 \[Distributed] TriangularDistribution[{-4, 3}, 2]}], u]Out[3]=
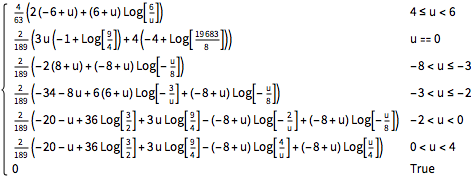
show complete Wolfram Language input
Out[4]=
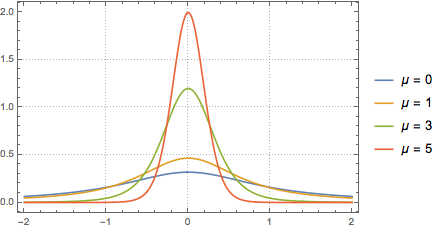
Find the PDF for the quotient of two independent normal random variables.
In[5]:=

pdf3 = PDF[
TransformedDistribution[
z1/z2, {z1 \[Distributed] NormalDistribution[],
z2 \[Distributed] NormalDistribution[\[Mu], 1]}], x]Out[5]=
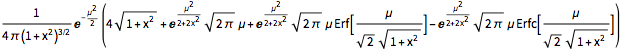
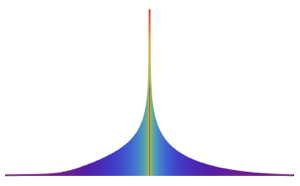
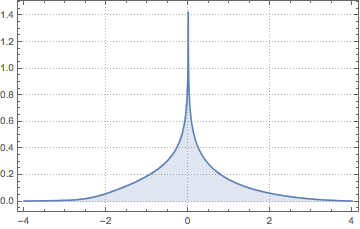
The distribution is heavy tailed for any fixed value of 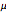 .
.
In[6]:=
Series[Exp[\[Mu]^2/2] pdf3, {x, Infinity, 8},
Assumptions -> \[Mu] > 0] // ExpandOut[6]=
show complete Wolfram Language input
Out[7]=