Densité de probabilité pour les produits et les quotients de variables aléatoires
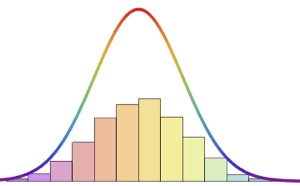
Trouvez la fonction de densité de probabilité pour le rapport entre l'échantillon le plus petit et le plus grand parmi les  dessins indépendants à partir de BetaDistribution[2, 3].
dessins indépendants à partir de BetaDistribution[2, 3].
In[1]:=

n = 5;
pdf = PDF[
TransformedDistribution[
min/max, {min, max} \[Distributed]
OrderDistribution[{BetaDistribution[2, 3], n}, {1, n}]], u]Out[1]=
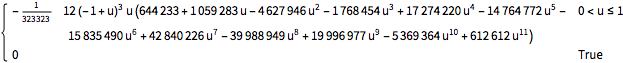
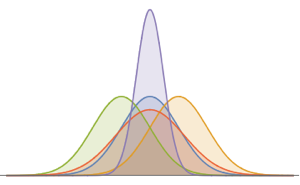
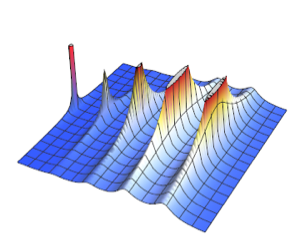
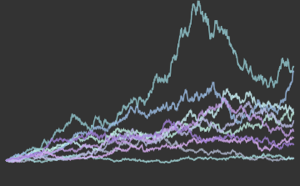
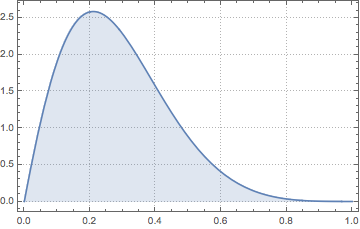
Visualisez la densité.
In[2]:=
Plot[pdf, {u, 0, 1}, PlotRange -> All, Filling -> Axis,
PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]Out[2]=
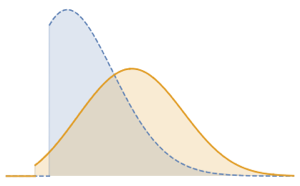
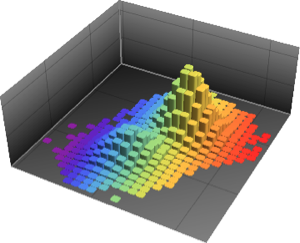
Calculez la densité de probabilité pour le produit de deux distributions triangulaires.
In[3]:=

pdf2 = PDF[
TransformedDistribution[
x1 x2, {x1 \[Distributed] TriangularDistribution[{-1, 2}, -1],
x2 \[Distributed] TriangularDistribution[{-4, 3}, 2]}], u]Out[3]=
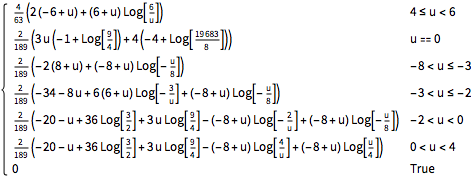
Afficher l'entrée complète de Wolfram Language
Out[4]=
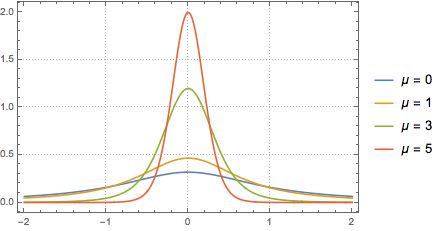
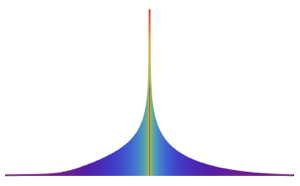
Trouvez la densité de probabilité pour le quotient de deux variables aléatoires normales indépendantes.
In[5]:=

pdf3 = PDF[
TransformedDistribution[
z1/z2, {z1 \[Distributed] NormalDistribution[],
z2 \[Distributed] NormalDistribution[\[Mu], 1]}], x]Out[5]=
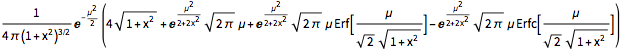
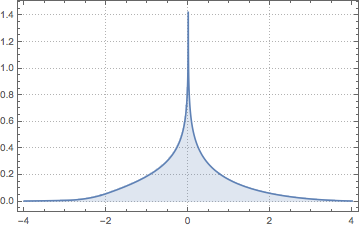
La distribution est à queue lourde pour toute valeur fixe de 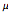 .
.
In[6]:=
Series[Exp[\[Mu]^2/2] pdf3, {x, Infinity, 8},
Assumptions -> \[Mu] > 0] // ExpandOut[6]=
Afficher l'entrée complète de Wolfram Language
Out[7]=