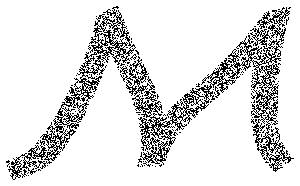領域からのサンプル点

RandomPointは，指定の領域における疑似乱数点の集合を一様にサンプリングする．

In[1]:=

Graphics[{Polygon[CirclePoints[5]], White, Point[RandomPoint[Polygon[CirclePoints[5]], 200]]}, ImageSize -> Medium]

Out[1]=

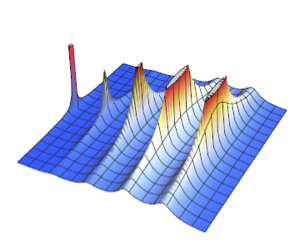
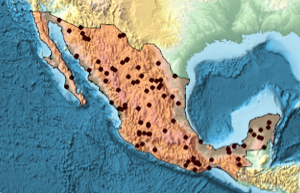
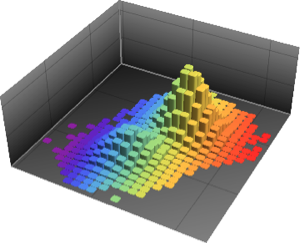
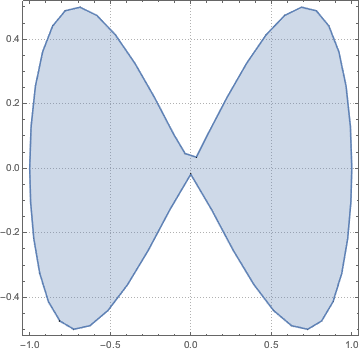
陰的なリサージュ(Lissajous)領域内のサンプル点．

In[2]:=

\[ScriptCapitalR] = ImplicitRegion[-1 + (-1 + 18 x^2 - 48 x^4 + 32 x^6)^2 + (-1 + 18 y^2 - 48 y^4 + 32 y^6)^2 <= 0, {x, y}];

In[3]:=

Graphics[{PointSize[Tiny], Point[RandomPoint[\[ScriptCapitalR], 10^4]]}, ImageSize -> Medium]

Out[3]=

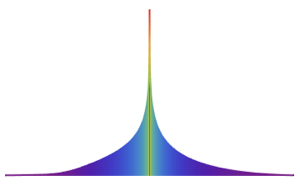
Textプリミティブからのサンプル点．

In[4]:=

mr = DiscretizeGraphics[Text[Style["\[CapitalSigma]", Bold]], _Text, MaxCellMeasure -> 0.1];

In[5]:=

Graphics[{PointSize[Tiny], Point[RandomPoint[mr, 10000]]}, ImageSize -> Medium]

Out[5]=

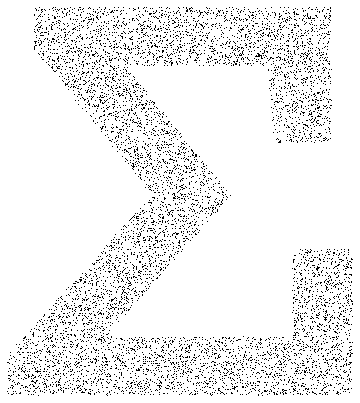
モンテカルロ（Monte Carlo）法を使って，パラメトリック領域における範囲での積分を近似する．

In[6]:=

region = ParametricRegion[{{s, s t}, s^2 + t^2 <= 1}, {s, t}];

In[7]:=

RegionPlot[region, ImageSize -> Medium, PlotTheme -> "Detailed", PlotLegends -> None]

Out[7]=

範囲内で積分される関数．

In[8]:=

f[{x_, y_}] := x^3 - 2 x^2 y + 4 x^6 - y^5; val = NIntegrate[f[{x, y}], {x, y} \[Element] region]

Out[8]=

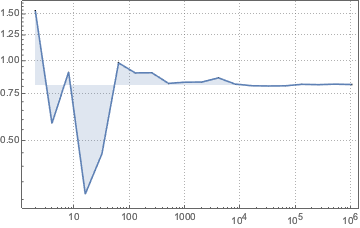
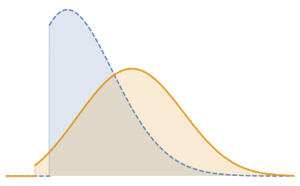
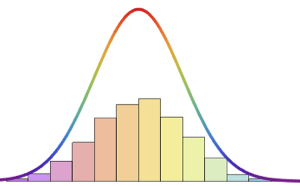
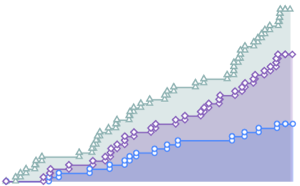
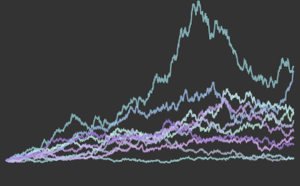
サンプルサイズの増加に伴うモンテカルロ統計の収束を可視化する．

In[9]:=

ListLogLogPlot[ Transpose[{2^Range[20], ParallelTable[ RegionMeasure[region] Mean[f /@ RandomPoint[region, 2^n]], {n, 1, 20}]}], PlotRange -> All, PlotTheme -> "Detailed", ImageSize -> Medium, Joined -> True, Filling -> val]

Out[9]=