領域上での偏微分方程式の感度を計算する
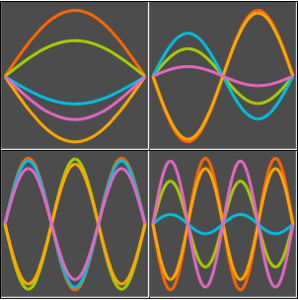
波動方程式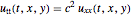 
, 
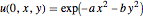のパラメトリック依存性を計算する．
波動方程式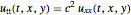 
を指定する．
In[1]:=
eqn = D[u[t, x, y], t, t] == c^2 Laplacian[u[t, x, y], {x, y}];初期条件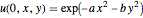 
を指定する．
In[2]:=
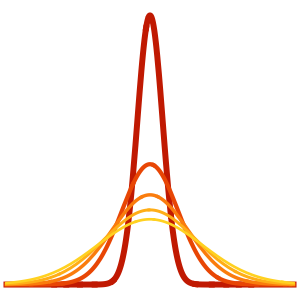
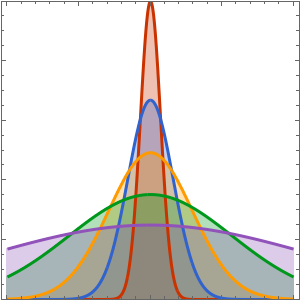
ics = {u[0, x, y] == Exp[-((a x)^2 + (b x)^2)],
Derivative[1, 0, 0][u][0, x, y] == 0};ディリクレの固定境界条件を指定する．
In[3]:=
bcs = DirichletCondition[u[t, x, y] == 0, True];パラメトリック関数を設定する．
In[4]:=
pfun = ParametricNDSolveValue[{eqn, ics, bcs},
u, {t, 0, 5}, {x, y} \[Element] Disk[], {a, b, c}];パラメータ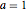 
，
，
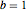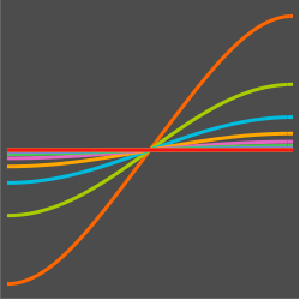
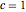について感度
，
，
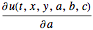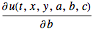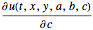を求める．
In[5]:=
ifda = D[pfun[a, 1, 1], a] /. {a -> 1};
ifda = D[pfun[1, b, 1], b] /. {b -> 1};
ifdc = D[pfun[1, 1, c], c] /. {c -> 1};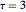
における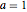 
，
，
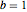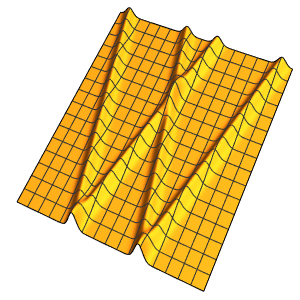
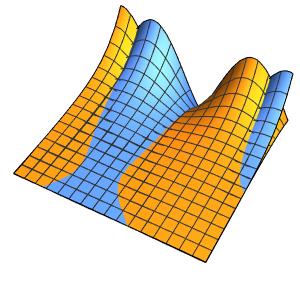
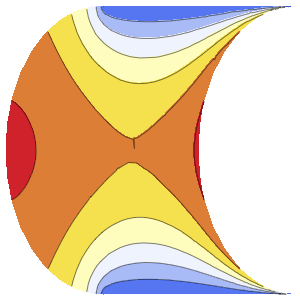
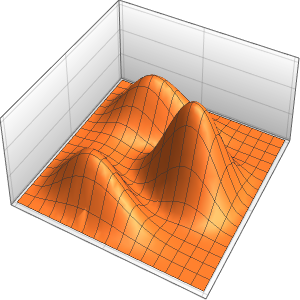
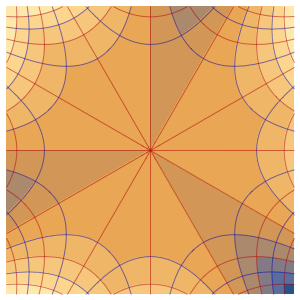
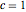のパラメトリック関数をプロットし，感度の
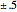を解に重ね合せることによって，対応する感度帯を可視化する．
In[6]:=
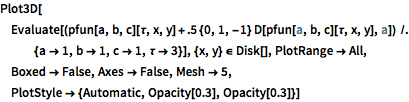
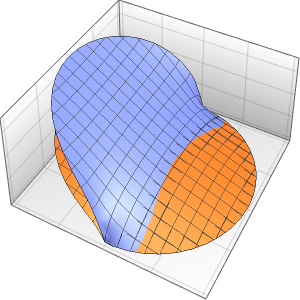
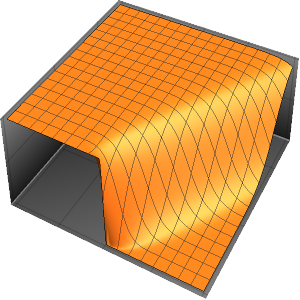
Plot3D[Evaluate[(pfun[a, b, c][\[Tau], x,
y] + .5 {0, 1, -1} D[pfun[a, b, c][\[Tau], x, y], a]) /. {a ->
1, b -> 1, c -> 1, \[Tau] -> 3}], {x, y} \[Element] Disk[],
PlotRange -> All, Boxed -> False, Axes -> False, Mesh -> 5,
PlotStyle -> {Automatic, Opacity[0.3], Opacity[0.3]}]Out[6]=
