计算区域中偏微分方程的灵敏度
计算波动方程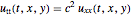 
, 
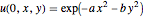的参数相关性.
指定波动方程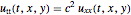 
.
In[1]:=
eqn = D[u[t, x, y], t, t] == c^2 Laplacian[u[t, x, y], {x, y}];指定初始条件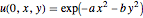 
.
In[2]:=
ics = {u[0, x, y] == Exp[-((a x)^2 + (b x)^2)],
Derivative[1, 0, 0][u][0, x, y] == 0};指定固定的狄利克雷边界条件.
In[3]:=
bcs = DirichletCondition[u[t, x, y] == 0, True];设定参数函数.
In[4]:=
pfun = ParametricNDSolveValue[{eqn, ics, bcs},
u, {t, 0, 5}, {x, y} \[Element] Disk[], {a, b, c}];求解灵敏度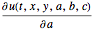 
、
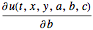和 
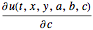，其中参数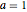 
， 
，
.
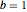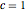In[5]:=
ifda = D[pfun[a, 1, 1], a] /. {a -> 1};
ifda = D[pfun[1, b, 1], b] /. {b -> 1};
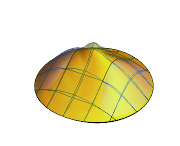
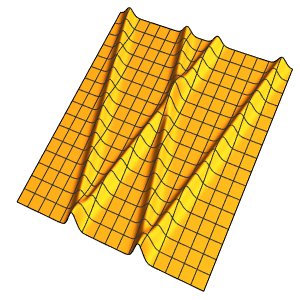
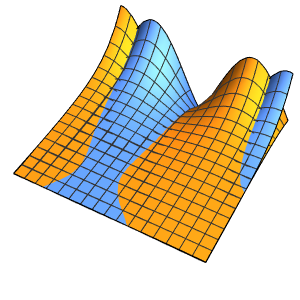
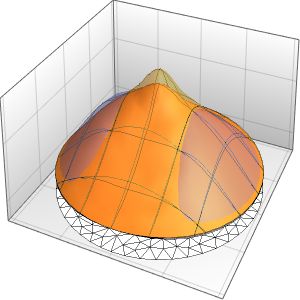
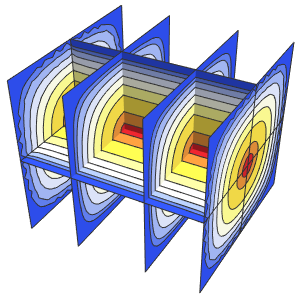
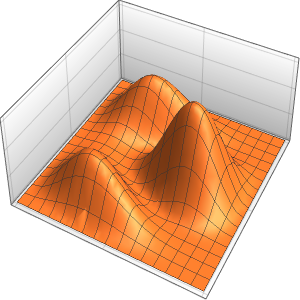
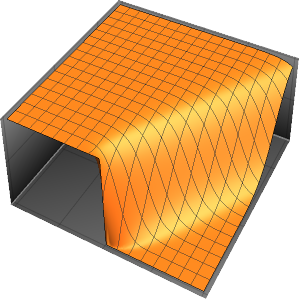
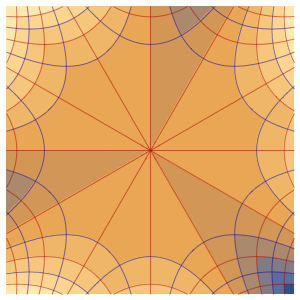
ifdc = D[pfun[1, 1, c], c] /. {c -> 1};通过绘制参数方程在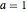 
，
， 
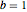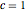和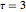 
时的图，并用灵敏度 
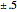覆盖在方程的解上，来可视化相应的灵敏度带（sensitivity bands）.
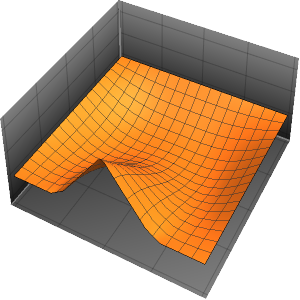
In[6]:=
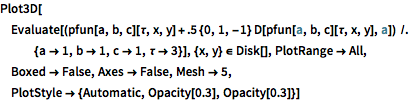
Plot3D[Evaluate[(pfun[a, b, c][\[Tau], x,
y] + .5 {0, 1, -1} D[pfun[a, b, c][\[Tau], x, y], a]) /. {a ->
1, b -> 1, c -> 1, \[Tau] -> 3}], {x, y} \[Element] Disk[],
PlotRange -> All, Boxed -> False, Axes -> False, Mesh -> 5,
PlotStyle -> {Automatic, Opacity[0.3], Opacity[0.3]}]Out[6]=
