构建复解析函数
从其在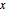 
轴上值的实部和虚部开始构建复解析函数.
实部和虚部 u 和 v 满足柯西-黎曼（Cauchy–Riemann）方程.
In[1]:=
creqns = {D[u[x, y], x] == D[v[x, y], y],
D[v[x, y], x] == -D[u[x, y], y]};规定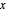 
轴上的 u 和 v 值.
In[2]:=
xvals = {u[x, 0] == x^3, v[x, 0] == 0};求解柯西-黎曼方程.
In[3]:=
sol = DSolve[{creqns, xvals}, {u, v}, {x, y}]Out[3]=
验证方程解为调和函数.
In[4]:=
Laplacian[{u[x, y], v[x, y]} /. sol[[1]], {x, y}]Out[4]=
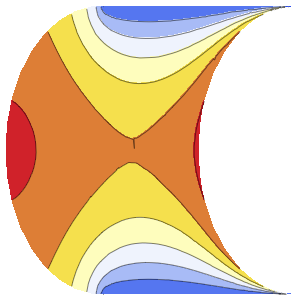
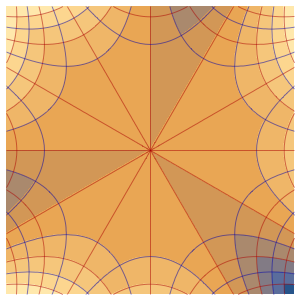
可视化方程解生成的流线和等势线.
In[5]:=
ContourPlot[{u[x, y], v[x, y]} /. sol[[1]], {x, -5, 5}, {y, -5, 5},
ContourStyle -> {Red, Blue}]Out[5]=
有方程的解构建一个复解析函数.
In[6]:=
f[x_, y_] = u[x, y] + I v[x, y] /. sol[[1]]Out[6]=
这代表了函数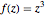 
.
In[7]:=
(f[x, y] // Factor) /. {x + I y -> z}Out[7]=
