ヨーロッパ型コールオプションの値を求める
原資産価格と行使価格がどちらも$100で,非危険利子率が6%,原資産の予想変動率が20%,満期が1年である場合の,ヨーロッパ型バニラコールオプションの値をブラック・ショールズ(Black–Scholes)モデルを使って求める.
In[1]:=
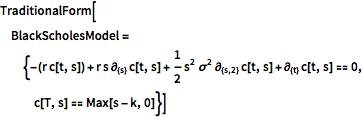
TraditionalForm[BlackScholesModel = {-(r c[t, s]) + r s \!\(
\*SubscriptBox[\(\[PartialD]\), \({s}\)]\(c[t, s]\)\) +
1/2 s^2 \[Sigma]^2 \!\(
\*SubscriptBox[\(\[PartialD]\), \({s, 2}\)]\(c[t, s]\)\) + \!\(
\*SubscriptBox[\(\[PartialD]\), \({t}\)]\(c[t, s]\)\) == 0,
c[T, s] == Max[s - k, 0]}]Out[1]//TraditionalForm=
境界値問題を解く.
In[2]:=
(dsol = c[t, s] /.
DSolve[BlackScholesModel, c[t, s], {t, s}][[
1]]) // TraditionalFormOut[2]//TraditionalForm=
ヨーロッパ型バニラオプションの値を計算する.
In[3]:=
dsol /. {t -> 0, s -> 100, k -> 100, \[Sigma] -> 0.2, T -> 1,
r -> 0.06}Out[3]=
FinancialDerivativeで与えられる値と比べる.
In[4]:=

FinancialDerivative[{"European", "Call"}, {"StrikePrice" -> 100.00,
"Expiration" -> 1}, {"InterestRate" -> 0.06, "Volatility" -> 0.2 ,
"CurrentPrice" -> 100}]Out[4]=