Bestimmen Sie den Wert einer europäischen Kaufoption

Bestimmen Sie den Wert einer europäischen Kaufoption bei einem Basiswert und einem Ausübungspreis von 100 $, einem risikofreien Zinssatz von 6%, einer Volatilität des Basiswerts von 20%, und einer Optionslaufzeit von 1 Jahr. Verwenden Sie dazu das Black–Scholes-Modells.

In[1]:=

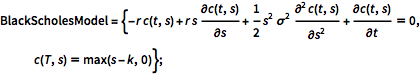
BlackScholesModel = {-r c(t, s) + r s \[PartialD]c(t, s)/\[PartialD]s + 1/2 s^2 \[Sigma]^2 \[PartialD]^2c(t, s)/\[PartialD]s^2 + \[PartialD]c(t, s)/\[PartialD]t == 0, c(T, s) == max(s - k, 0)};

Lösen Sie das Anfangswertproblem.

In[2]:=

(dsol = c[t, s] /. DSolve[BlackScholesModel, c[t, s], {t, s}][[ 1]]) // TraditionalForm

Out[2]//TraditionalForm=

Berechnen Sie den Wert der europäischen Kaufoption.

In[3]:=

dsol /. {t -> 0, s -> 100, k -> 100, \[Sigma] -> 0.2, T -> 1, r -> 0.06}

Out[3]=

Vergleichen Sie diesen mit dem von FinancialDerivative berechneten Wert.

In[4]:=

FinancialDerivative[{"European", "Call"}, {"StrikePrice" -> 100.00, "Expiration" -> 1}, {"InterestRate" -> 0.06, "Volatility" -> 0.2 , "CurrentPrice" -> 100}]

Out[4]=