求解基本施图姆-刘维尔问题

求解带有狄利克雷条件的特征值问题.

In[1]:=

sol = DSolve[{y''[x] + \[Lambda] y[x] == 0, y[0] == 0, y[\[Pi]] == 0}, y[x], x]

Out[1]=

制作前五个特征函数的表格.

In[2]:=

eigfuns = Table[y[x] /. sol[[1]] //. {\[FormalN] -> i, \[Lambda] -> \[FormalN]^2} /. {C[ 1] -> 1}, {i, 5}]

Out[2]=

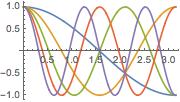
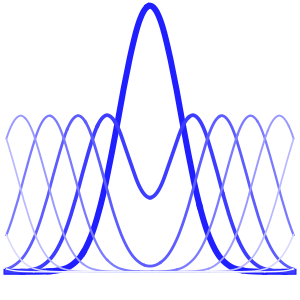
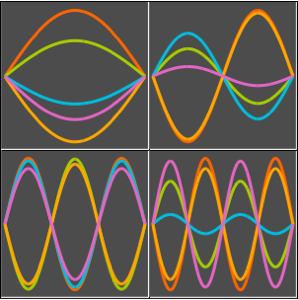
绘制这些特征函数.

In[3]:=

Plot[Evaluate[eigfuns], {x, 0, Pi}]

Out[3]=

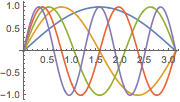
求解带有诺依曼（Neumann）条件的特征值问题.

In[4]:=

sol = DSolve[{y''[x] + \[Lambda] y[x] == 0, y'[0] == 0, y'[\[Pi]] == 0}, y[x], x]

Out[4]=

制作前五个特征函数的表格.

In[5]:=

eigfuns = Table[y[x] /. sol[[1]] //. {\[FormalN] -> i, \[Lambda] -> \[FormalN]^2} /. {C[ 1] -> 1}, {i, 5}]

Out[5]=

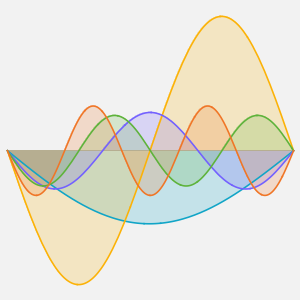
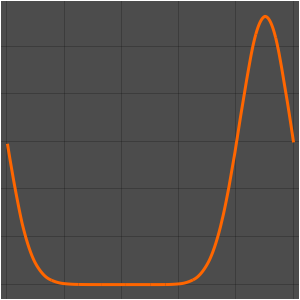
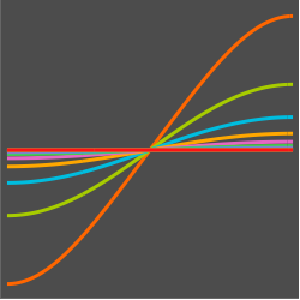
绘制这些特征函数.

In[6]:=

Plot[Evaluate[eigfuns], {x, 0, Pi}]

Out[6]=