ヘルムホルツ方程式のディリクレ問題を解く

二次元のヘルムホルツ(Helmholtz)方程式を指定する．

In[1]:=

heqn = {Laplacian[u[x, y], {x, y}] + 5 u[x, y] == 0};

長方形内の方程式についてディリクレ条件を与える．

In[2]:=

bc = {u[x, 0] == UnitTriangle[x - 2]/2, u[x, 2] == 0, u[0, y] == 0, u[4, y] == 0};

DSolveValueを使ってディリクレ問題を解く．

In[3]:=

(sol = DSolveValue[{heqn, bc}, u[x, y], {x, y}]) // TraditionalForm

Out[3]//TraditionalForm=

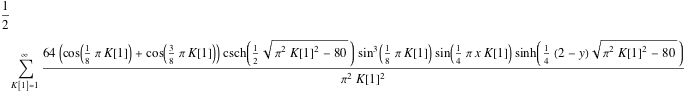
Inactiveの和から最初の30項を取り出す．

In[4]:=

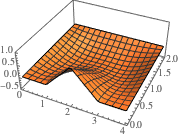
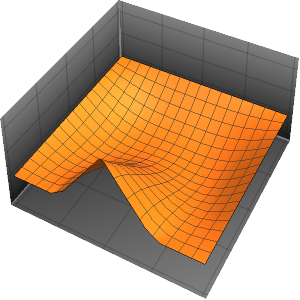
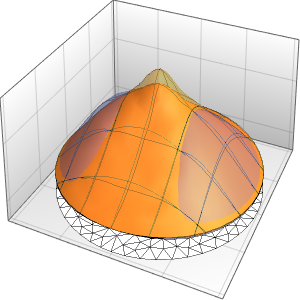
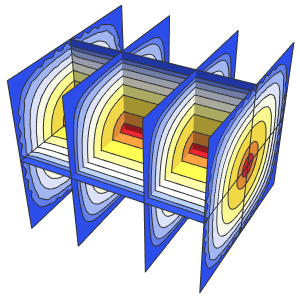
fsol = sol /. \[Infinity] -> 30 // Activate;

近似解を可視化する．

In[5]:=

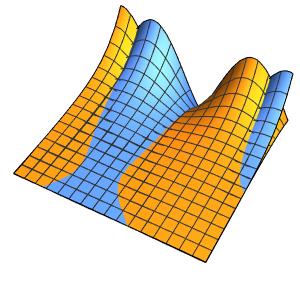
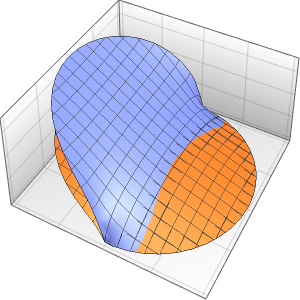
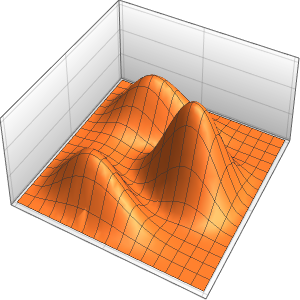
Plot3D[fsol // Evaluate, {x, 0, 4}, {y, 0, 2}, PlotRange -> All, PlotTheme -> "Scientific"]

Out[5]=