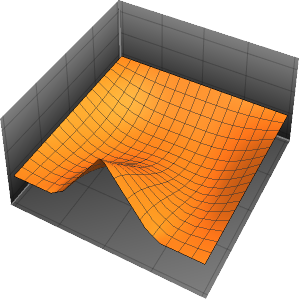
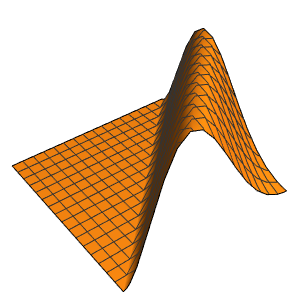
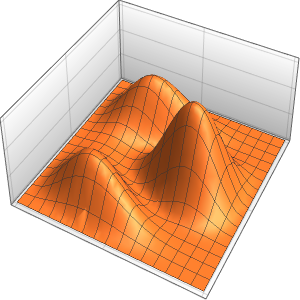
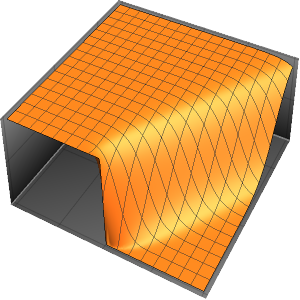
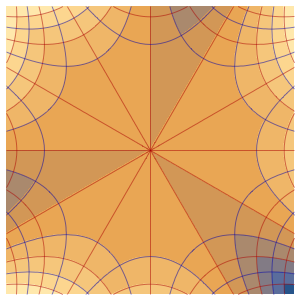
求解带有周期性边界条件的波动方程
求解一维带有周期性边界条件的波动方程.
指定一个带有吸收边界条件的波动方程. 注意诺依曼（Neumann）值是用于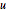 
的一阶时间导数的.
In[1]:=
eqn = D[u[t, x], {t, 2}] ==
D[u[t, x], {x, 2}] +
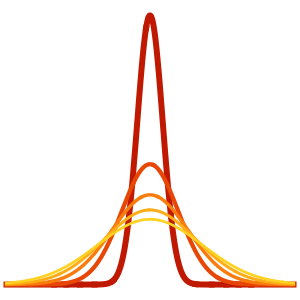
NeumannValue[-Derivative[1, 0][u][t, x], x == 0 || x == 1];指定波动方程的初始条件.
In[2]:=
f[x_] = D[0.125 Erf[(x - 0.5)/0.125], x];
vInit[x_] = -D[f[x], x];
ic = {u[0, x] == f[x], Derivative[1, 0][u][0, x] == vInit[x]};指定一个周期性边界条件，使得右边界的方程解会传播到左边.
In[3]:=
bc = PeriodicBoundaryCondition[u[t, x], x == 0,
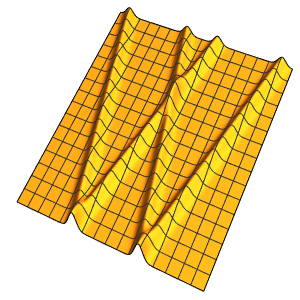
TranslationTransform[{1}]];使用有限元方法求解方程.
In[4]:=
ufun = NDSolveValue[{eqn, ic, bc}, u, {t, 0, 2}, {x, 0, 1},
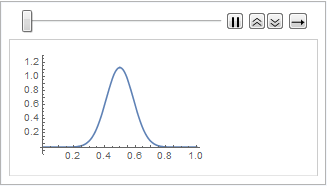
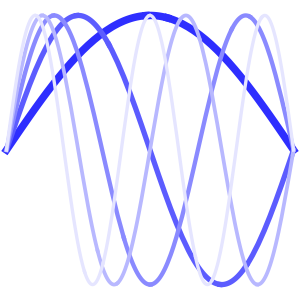
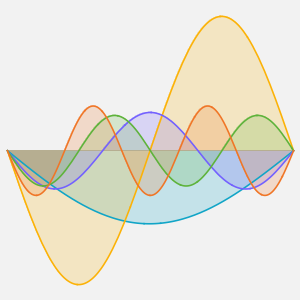
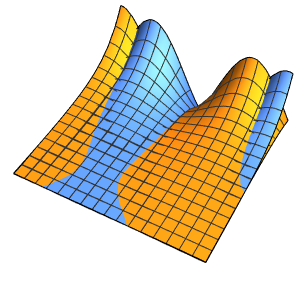
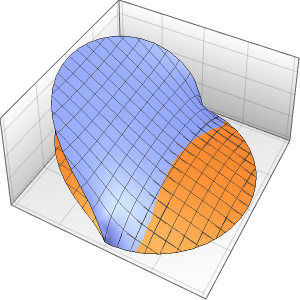
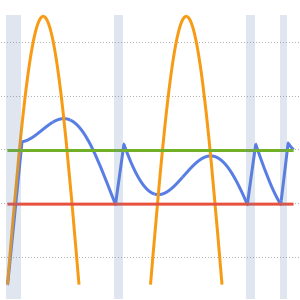
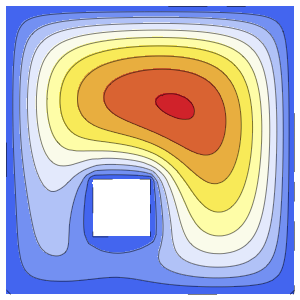
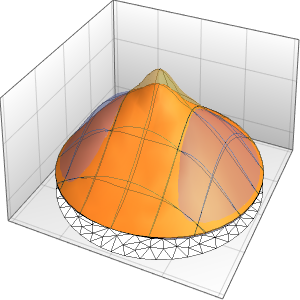
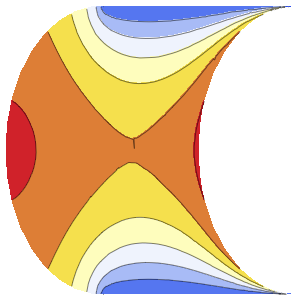
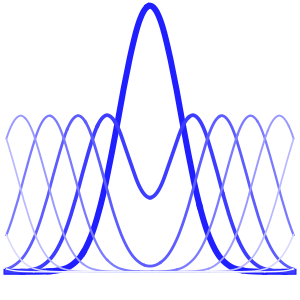
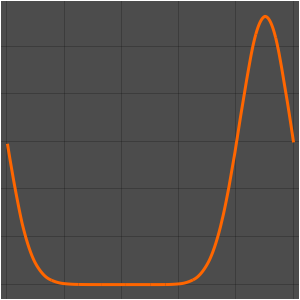
Method -> {"MethodOfLines"}];可视化周期性波动函数.
In[5]:=
plots = Table[
Plot[ufun[t, x], {x, 0, 1}, PlotRange -> {-0.1, 1.3}], {t, 0,
2, .1}];
ListAnimate[plots]
